题目内容
求值：
（1）sin163°sin223°+sin253°sin313°
（2）
．
（1）sin163°sin223°+sin253°sin313°
（2）
| tan330°•cos(-315°)•cos420° |
| cot(-600°)•sin1050° |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：（1）原式利用诱导公式变形后，再利用两角和与差的余弦函数公式化简，即可求出值；
（2）原式利用诱导公式化简后，计算即可得到结果．
（2）原式利用诱导公式化简后，计算即可得到结果．
解答：
解：（1）原式=-sin17°sin43°+sin73°sin47°=-sin17°sin43°+cos17°cos43°=cos（43°+17°）=cos60°=
；
（2）原式=
=-
．
| 1 |
| 2 |
（2）原式=
| -tan30°cos45°cos60° | ||
|
| ||
| 2 |
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
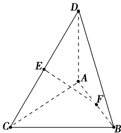已知DA⊥平面ABC，AC⊥CB，AC=CB=AD=2，E是DC的中点，F是AB的中点．
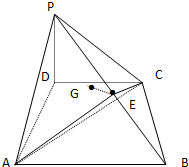如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠CDA=∠DAB=90°，PD⊥底面ABCD，PD=AD，CD=1，AB=2，E是PB中点，点E在平面ACP上的射影是△ACP