题目内容
已知：函数f（x）=2sin（2x-
）
（1）求函数的对称中心的坐标，对称轴方程；
（2）当x∈[0，π]时，求函数f（x）的单调递增区间．
| π |
| 3 |
（1）求函数的对称中心的坐标，对称轴方程；
（2）当x∈[0，π]时，求函数f（x）的单调递增区间．
考点：正弦函数的单调性,正弦函数的定义域和值域
专题：三角函数的图像与性质
分析：（1）分别令2x-
=kπ，2x-
=kπ+
解x可得所求；（2）令2kπ-
≤2x-
≤2kπ+
，解得x和[0，π]取交集可得．
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答：
解：（1）令2x-
=kπ可解得x=
+
，
2x-
=kπ+
可解得x=
+
，
∴函数图象的对称中心为：(
+
，0)，k∈Z，
对称轴方程为：x=
+
，k∈z；
（2）令2kπ-
≤2x-
≤2kπ+
，
解得kπ-
≤x≤kπ+
，k∈Z
∴当x∈[0，π]时，函数f（x）的单调递增区间为为：[0，
）和（
，π]
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
2x-
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
∴函数图象的对称中心为：(
| kπ |
| 2 |
| π |
| 6 |
对称轴方程为：x=
| kπ |
| 2 |
| 5π |
| 12 |
（2）令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得kπ-
| π |
| 12 |
| 5π |
| 12 |
∴当x∈[0，π]时，函数f（x）的单调递增区间为为：[0，
| 5π |
| 12 |
| 11π |
| 12 |
点评：本题考查正弦函数的单调性和对称性，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
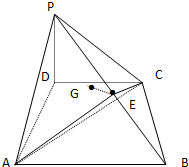如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠CDA=∠DAB=90°，PD⊥底面ABCD，PD=AD，CD=1，AB=2，E是PB中点，点E在平面ACP上的射影是△ACP