题目内容
（1）在△ABC中，sinA=
，cosB=
，求cosC的值．
（2）已知cos（
+x）=
，
π＜x＜
π，求
的值．
| 5 |
| 13 |
| 3 |
| 5 |
（2）已知cos（
| π |
| 4 |
| 3 |
| 5 |
| 17 |
| 12 |
| 7 |
| 4 |
| sin2x+2sin2x |
| 1-tanx |
考点：两角和与差的余弦函数,三角函数的化简求值,二倍角的正弦,二倍角的余弦
专题：三角函数的求值
分析：（1）根据已知条件，求解cosA=
，sinB=
，然后，借助于诱导公式进行求解；
（2）首先，化简给定的式子，然后，根据已知条件，变形求值．
| 12 |
| 13 |
| 4 |
| 5 |
（2）首先，化简给定的式子，然后，根据已知条件，变形求值．
解答：
解：（1）∵在△ABC中，sinA=
，cosB=
，
∴cosA=
，sinB=
，
∴cosC=cos[π-（A+B）]
=-cos（A+B）
=-cosAcosB+sinAsinB
=-
×
+
×
=-
．
∴cosC=-
．
（2）∵
=
=
=
∵cos（
+x）=
，
π＜x＜
π，
∴sin（x+
）=-
，
∴2sinxcosx=
．
∴
=-
，
∴
=-
．
| 5 |
| 13 |
| 3 |
| 5 |
∴cosA=
| 12 |
| 13 |
| 4 |
| 5 |
∴cosC=cos[π-（A+B）]
=-cos（A+B）
=-cosAcosB+sinAsinB
=-
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
=-
| 16 |
| 65 |
∴cosC=-
| 16 |
| 65 |
（2）∵
| sin2x+2sin2x |
| 1-tanx |
| 2sinxcosx+2sin2x | ||
1-
|
=
| 2sinxcosx(cosx+sinx) |
| cosx-sinx |
=
2sinxcosxsin(x+
| ||
cos(x+
|
∵cos（
| π |
| 4 |
| 3 |
| 5 |
| 17 |
| 12 |
| 7 |
| 4 |
∴sin（x+
| π |
| 4 |
| 4 |
| 5 |
∴2sinxcosx=
| 41 |
| 50 |
∴
2sinxcosxsin(x+
| ||
cos(x+
|
| 28 |
| 75 |
∴
| sin2x+2sin2x |
| 1-tanx |
| 28 |
| 75 |
点评：本题重点考查了同角三角函数基本关系式，三角函数的性质．二倍角公式等知识，属于中档题．
练习册系列答案
相关题目
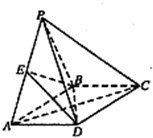如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，
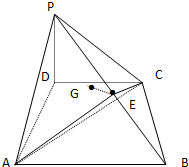如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠CDA=∠DAB=90°，PD⊥底面ABCD，PD=AD，CD=1，AB=2，E是PB中点，点E在平面ACP上的射影是△ACP