题目内容
已知等差数列{an}的前n项的和为Sn,a5+a6=11,S4=10.
(1)求数列{an}的通项公式;
(2)已知数列{bn}是首项为1,公比为2的等比数列,求数列{anbn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)已知数列{bn}是首项为1,公比为2的等比数列,求数列{anbn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:解题思想,解题方法,等差数列与等比数列
分析:(1)可利用等差数列{an}的通项公式an=a1+(n-1)d和前n项和公式Sn=na1+
来解决.
(2)可利用等比数列的通项公式bn=b1qn-1和错位相减法求数列的前n项和.
| n(n+1)d |
| 2 |
(2)可利用等比数列的通项公式bn=b1qn-1和错位相减法求数列的前n项和.
解答:
解:(1)∵等差数列{an}的前n项的和为Sn,a5+a6=11,S4=10,
∴
,
∴
,
∴
,
∴数列{an}的通项公式为an=n.
(2)∵数列{bn}是首项为1,公比为2的等比数列,
∴bn=2n-1.
∵数列{anbn}的前n项和Tn,
∴Tn=1+2×2+3×4+…+n×2n-1,
∴2Tn=2+2×22+3×23+…+n×2n,
两式相减得,
-Tn=1+2+22+23+…+2n-1-n•2n,
∴Tn=n•2n-(1+2+22+23+…+2n-1)=n•2n-
=(n-1)2n+1.
∴
|
∴
|
∴
|
∴数列{an}的通项公式为an=n.
(2)∵数列{bn}是首项为1,公比为2的等比数列,
∴bn=2n-1.
∵数列{anbn}的前n项和Tn,
∴Tn=1+2×2+3×4+…+n×2n-1,
∴2Tn=2+2×22+3×23+…+n×2n,
两式相减得,
-Tn=1+2+22+23+…+2n-1-n•2n,
∴Tn=n•2n-(1+2+22+23+…+2n-1)=n•2n-
| 1-2n |
| 1-2 |
点评:本题考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a>0,且a≠1,则“函数y=logax在(0,+∞)上是减函数”是“函数y=(2-a)x3在R上是增函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
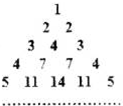 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.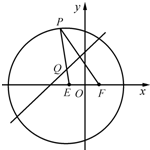 如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.