题目内容

双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与直线y=2x有公共点，则双曲线的离心率的取值范围是（　　）
A、（1，
5
）
B、（
5
，+∞）
C、（1，
5
]
D、[
5
，+∞）
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与直线y=2x有交点，应有
b
a
＞2，可得e的范围．
解答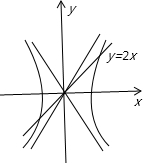： 解：如图所示，
∵双曲线的渐近线方程为y=±
b
a
x，双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）与直线y=2x有交点，
∴应有
b
a
＞2，
∴e=
1+(
b
a
)2
＞
5
．
故选：B．
点评：本题考查了双曲线的渐近线和离心率，直线与双曲线相交等问题，常用数形结合的方法来考虑，是基础题．
练习册系列答案
相关题目
等差数列{an}中，a2=5，a6=33，则a3+a5=（　　）
A、33B、28C、38D、52
设向量
a
=（cos25°，sin25°），
b
=（sin20°，cos20°），若t是实数，且
u
=
a
+t
b
，则|
u
|的最小值为（　　）
A、
2
B、
2
2
C、1
D、
1
2
下列四组函数中，表示同一函数的是（　　）
A、y=
x2
与y=
3x3
B、y=1与y=x0
C、y=2x+1与y=2t+1
D、y=x与y=(
x
)2
若函数f（x）=
1+lnx
x
在区间（a，a+
2
3
） （a≥0）上有极值，则实数a的取值范围是（　　）
A、（0，1）
B、（
2
3
，1）
C、（
1
2
，1）
D、（
1
3
，1）
给定下列四个命题：
①“x=
π
6
”是“sin x=
1
2
”的充分不必要条件；
②若“p∨q”为真，则“p∧q”为真；
③若a＜b，则am2＜bm2；    
④若集合A∩B=A，则A⊆B．
其中为真命题的是（　　）（填上所有正确命题的序号）．
A、.②④B、.①④
C、.①②D、.①③
已知映射f：M→N，使集合N中的元素y=x2与集合M中的元素x对应，要使映射f：M→N是一一对应，那么M，N可以是（　　）
A、M=R，N=R
B、M=R，N={y|y≥0}
C、M={x|x≥0}，N=R
D、M={x|x≥0}，N={y|y≥0}
周期为π的函数f（x）=2sin（ωx-
π
6
）-m（ω＞0）在x∈[0，
π
2
]上有两个零点，则实数m的取值范围为（　　）
A、（-2，2）
B、[1，2）
C、[-1，2]
D、（0，2）
化简求值．
（1）
327
+(-
1
2
)-2+(1
7
9
)
1
2
-(
2
-1)0
（2）lg500+lg
8
5
-
1
2
lg64+50（lg2+lg5）2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网