题目内容
已知函数f（x）=
．
（1）求证：函数f（x）的图象的对称中心是（
，
）；
（2）求f（
）+f（
）+…+f（
）的值．
| 4x |
| 4x+2 |
（1）求证：函数f（x）的图象的对称中心是（
| 1 |
| 2 |
| 1 |
| 2 |
（2）求f（
| 1 |
| 101 |
| 2 |
| 101 |
| 100 |
| 101 |
考点：指数型复合函数的性质及应用
专题：函数的性质及应用
分析：（1）由已知中函数的解析式，分析出1-f（1-x）=f（x），可得函数f（x）的图象的对称中心是（
，
）；
（2）由（1）得：f（x）+f（1-x）=1，进而可得f（
）+f（
）+…+f（
）=50f（x）+f（1-x）．
| 1 |
| 2 |
| 1 |
| 2 |
（2）由（1）得：f（x）+f（1-x）=1，进而可得f（
| 1 |
| 101 |
| 2 |
| 101 |
| 100 |
| 101 |
解答：
证明：（1）∵函数f（x）=
．
∴1-f（1-x）=1-
=
=
=
=
，
故函数f（x）的图象的对称中心是（
，
）；
解：（2）由（1）得：f（x）+f（1-x）=1，
∴f（
）+f（
）+…+f（
）=50
| 4x |
| 4x+2 |
∴1-f（1-x）=1-
| 41-x |
| 41-x+2 |
| 41-x+2-41-x |
| 41-x+2 |
| 2 |
| 41-x+2 |
| 2•4x |
| 4 +2•4x |
| 4x |
| 4x+2 |
故函数f（x）的图象的对称中心是（
| 1 |
| 2 |
| 1 |
| 2 |
解：（2）由（1）得：f（x）+f（1-x）=1，
∴f（
| 1 |
| 101 |
| 2 |
| 101 |
| 100 |
| 101 |
点评：本题考查的知识点是函数的对称性，其中熟练掌握函数对称变换法则，是解答的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
设集合A={α|α=k•180°+90°，k∈z}∪{α|α=k•180°，k∈z}，集合B={β|β=k•90°，k∈z}，则（ ）
| A、A?B | B、A?B |
| C、A∩B=∅ | D、A=B |
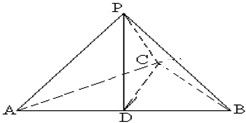如图，已知三棱锥P-ABC，D为AB的中点，且△PDB是正三角形，PA⊥PC．求证：PC⊥BC．
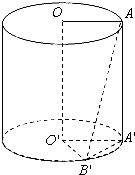圆柱的高为4cm，底面半径为3cm，上底面一条半径OA与下底面一条半径O′B′成60°角，求：