题目内容
若抛物线y2=2px上的三点的纵坐标的平方成等差数列,则这三点到焦点的对应距离构成的数列是 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先设三点的坐标,根据纵坐标的平方成等差数列可得到其横坐标也成等差数列,然后表示出三点到焦点的距离,即可得到答案.
解答:
解:设这三点为A(x1,y1)B(x2,y2)C(x3,y3)
因为纵坐标的平方成等差数列,即 y12,y22,y32成等差数列,三点纵坐标分别代入抛物线方程,
可知三点横坐标亦成等差数列.
即2x2=x1+x2,
因为AF=x1+
,BF=x2+
,CF=x3+
AF+CF=x1+x3+
+
=x1+x3+p=2x2+p=2BF
所以2BF=AF+CF
故三点到焦点的对应距离构成的数列是等差数列.
故答案为:等差数列.
因为纵坐标的平方成等差数列,即 y12,y22,y32成等差数列,三点纵坐标分别代入抛物线方程,
可知三点横坐标亦成等差数列.
即2x2=x1+x2,
因为AF=x1+
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
AF+CF=x1+x3+
| p |
| 2 |
| p |
| 2 |
所以2BF=AF+CF
故三点到焦点的对应距离构成的数列是等差数列.
故答案为:等差数列.
点评:本题主要考查抛物线的基本性质,即抛物线上点到焦点的距离等于到准线的距离.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若复数a=3+2i,b=4+mi,要使复数
为纯虚数,则实数m的值为( )
| a |
| b |
| A、-6 | ||
| B、6 | ||
C、
| ||
D、-
|
已知b为如图所示的程序框图输出的结果,则二项式(
-
)6的展开式中的常数项是( )

| bx |
| 1 | ||
|

| A、-20 | B、20 |
| C、-540 | D、540 |
 已知正四棱锥V-ABCD可绕着AB任意旋转,CD∥平面α.若AB=2,VA=
已知正四棱锥V-ABCD可绕着AB任意旋转,CD∥平面α.若AB=2,VA=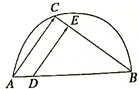 如图,半圆的直径AB=6,C是半圆上的一点,D、E分别是AB、BC上的点,且AD=1,BE=4,DE=3.
如图,半圆的直径AB=6,C是半圆上的一点,D、E分别是AB、BC上的点,且AD=1,BE=4,DE=3.