题目内容
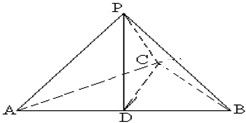 如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.
如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:在三角形PAB中,根据中线PD=
AB,证出PA⊥PB.再结合PA⊥PC,利用线面垂直的判定定理证出AP⊥平面PBC,从而得到AP⊥BC,可证平面PAC⊥平面ABC,从而证出BC⊥平面PAC,即可证明PC⊥BC.
| 1 |
| 2 |
解答:
证明:∵D是AB的中点,△PDB是正三角形,设AB=2,
∴AD=PD=DB=PB=1,由余弦定理知AP=
=
.…(5分)
∴AP2=AB2+PB2,△PAB是直角三角形,且AP⊥PB,…(6分)
又∵AP⊥PC,PB∩PC=P,PB、PC?平面PBC
∴AP⊥平面PBC. …(8分)
∵AP?平面APC.
∴平面PAC⊥平面ABC.…(10分)
∵BC⊥AP,AP∩CP=P,AP、PC?平面PAC
∴BC⊥PC.…(12分)
∴AD=PD=DB=PB=1,由余弦定理知AP=
| 12+12-2cos120° |
| 3 |
∴AP2=AB2+PB2,△PAB是直角三角形,且AP⊥PB,…(6分)
又∵AP⊥PC,PB∩PC=P,PB、PC?平面PBC
∴AP⊥平面PBC. …(8分)
∵AP?平面APC.
∴平面PAC⊥平面ABC.…(10分)
∵BC⊥AP,AP∩CP=P,AP、PC?平面PAC
∴BC⊥PC.…(12分)
点评:本题主要考察了直线与平面垂直的性质,属于基本知识的考查.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设f(x)=
,则f(f(-4))=( )
|
| A、1 | B、-2 | C、-1 | D、2 |
 已知正四棱锥V-ABCD可绕着AB任意旋转,CD∥平面α.若AB=2,VA=
已知正四棱锥V-ABCD可绕着AB任意旋转,CD∥平面α.若AB=2,VA=