题目内容
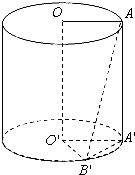 圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求:
圆柱的高为4cm,底面半径为3cm,上底面一条半径OA与下底面一条半径O′B′成60°角,求:(1)直线AB′与圆柱的轴OO′所成的角(用反三角函数值表示);
(2)直线AB′与平面OAA′O′所成角的大小;
(3)点A沿圆柱侧面到达点B′的最短距离.
考点:直线与平面所成的角,多面体和旋转体表面上的最短距离问题,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)由OO′∥AA′,得∠B′AA′是所求异面直线AB′与OO′所成角或其补角,由此能求出异面直线AB′与OO′所成角的大小.
(2)过B′作B′H⊥O′A′于点H,由已知得∠B′AH即为所求的线面角,由此能求出直线AB′与平面OAA′O′所成角的大小.
(3)将圆柱的侧面沿过B ′ 的母线展开,与AA′构成以π为长4为宽的矩形,|
|min即为此矩形的对角线长,由此能求出点A沿圆柱侧面到达点B′的最短距离.
(2)过B′作B′H⊥O′A′于点H,由已知得∠B′AH即为所求的线面角,由此能求出直线AB′与平面OAA′O′所成角的大小.
(3)将圆柱的侧面沿过B ′ 的母线展开,与AA′构成以π为长4为宽的矩形,|
 |
| AB′ |
解答:
解:(1)∵OO′∥AA′,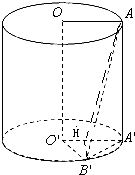
∴∠B′AA′是所求异面直线AB′与OO′所成角或其补角,
由题意知△OA′B′为等边三角形,且AA′⊥A′B′,
∴|A′B′|=3,|AA′|=4,
即∠B′AA′=arctan
,
∴异面直线AB′与OO′所成角的大小为arctan
.
(2)过B′作B′H⊥O′A′与点H,
则B′H⊥O′A′,B′H⊥AA′,
∴B′H⊥平面OAA′O′,
∴AH为直线AB′在平面OAA′O′上的射影,
∴∠B′AH即为所求的线面角,
∵B′H=
,AA′=5,
∴∠B′AH=arcsin
,
∴直线AB′与平面OAA′O′所成角的大小为arcsin
.
(3)将圆柱的侧面沿过B ′ 的母线展开,
与AA′构成以π为长4为宽的矩形,
|
|min即为此矩形的对角线长,
∴|
|min=
,
故点A沿圆柱侧面到达点B′的最短距离为
.

∴∠B′AA′是所求异面直线AB′与OO′所成角或其补角,
由题意知△OA′B′为等边三角形,且AA′⊥A′B′,
∴|A′B′|=3,|AA′|=4,
即∠B′AA′=arctan
| 3 |
| 4 |
∴异面直线AB′与OO′所成角的大小为arctan
| 3 |
| 4 |
(2)过B′作B′H⊥O′A′与点H,
则B′H⊥O′A′,B′H⊥AA′,
∴B′H⊥平面OAA′O′,
∴AH为直线AB′在平面OAA′O′上的射影,
∴∠B′AH即为所求的线面角,
∵B′H=
3
| ||
| 2 |
∴∠B′AH=arcsin
3
| ||
| 10 |
∴直线AB′与平面OAA′O′所成角的大小为arcsin
3
| ||
| 10 |
(3)将圆柱的侧面沿过B ′ 的母线展开,
与AA′构成以π为长4为宽的矩形,
|
 |
| AB′ |
∴|
 |
| AB′ |
| 16+π2 |
故点A沿圆柱侧面到达点B′的最短距离为
| 16+π2 |
点评:本题考查异面直线所成角的求法,考查直线与平面所成的角的求法,考查点A沿圆柱侧面到达点B′的最短距离的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目