题目内容
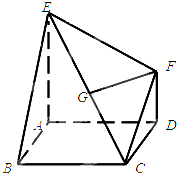 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.(1)求多面体EABCDF的体积;
(2)若FG⊥EC于G,求证:FG∥面ABCD.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)首先,连接ED,多面体EABCDF的体积V=VE-PCD+VE-ABCD ,只有分别求解两个棱锥的体积即可;
(2)设AC与BD相交于点O,连结OG,只需证明四边形DOGF为平行四边形即可.
(2)设AC与BD相交于点O,连结OG,只需证明四边形DOGF为平行四边形即可.
解答:
 解:(1)连接ED,
解:(1)连接ED,
∵EA⊥底面ABCD,FD∥EA,
∴FD⊥底面ABCD,
∴FD⊥AD,FD∩AD=D,
∴AD⊥平面FDC,
VE-PCD=
AD•S△FDC=
×
×1×2×2=
,
VE-ABCD=
EA•S正方形ABCD=
×2×2×2=
,
∴多面体EABCDF的体积V=VE-PCD+VE-ABCD
=
+
=
;
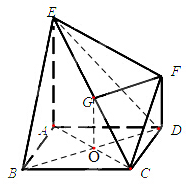
(2)设AC与BD相交于点O,连结OG.
∵OG是△AEC的中位线∴OG∥AE,且AE=2OG,
∵由已知EA=2FD,
∴OG∥DF且OG=DF,
可得平面四边形DOGF为平行四边形,
∴FG∥OD,
又∵FG?ABCD,OD?ABCD,
∴FG∥面ABCD.
 解:(1)连接ED,
解:(1)连接ED,∵EA⊥底面ABCD,FD∥EA,
∴FD⊥底面ABCD,
∴FD⊥AD,FD∩AD=D,
∴AD⊥平面FDC,
VE-PCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
VE-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
∴多面体EABCDF的体积V=VE-PCD+VE-ABCD
=
| 2 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
(2)设AC与BD相交于点O,连结OG.
∵OG是△AEC的中位线∴OG∥AE,且AE=2OG,
∵由已知EA=2FD,
∴OG∥DF且OG=DF,
可得平面四边形DOGF为平行四边形,
∴FG∥OD,
又∵FG?ABCD,OD?ABCD,
∴FG∥面ABCD.
点评:本题重点考查了空间中直线与直线平行、垂直,直线与平面平行垂直,面面垂直等判定和性质定理及其应用,空间中棱锥的体积计算等知识,属于重点题型,注意解决中点问题的一般思路:有中点取中点,相连得到中位线,本题属于中档题.

练习册系列答案
相关题目
 某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.
某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.