题目内容
若直线l:2ax-by+2=0(a>0,b>0)与x轴相交于点A,与y轴相交于B,被圆x2+y2+2x-4y+1=0截得的弦长为4,则|OA|+|OB|(O为坐标原点)的最小值为 .
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:把圆的方程化为标准方程后,找出圆心坐标和圆的半径,由直线被圆截得的弦长为4刚好为圆的直径,得到直线过圆心,所以把圆心坐标代入直线方程得到a+b的值,根据a+b的值,利用基本不等式即可|OA|+|OB|(O为坐标原点)的最小值.
解答:
解:圆x2+y2+2x-4y+1=0可化为(x+1)2+(y-2)2=4
∵直线l被圆x2+y2+2x-4y+1=0截得的弦长为4,
由直线被圆截取的弦长为4,圆的直径也为4,得到直线过圆心,
把圆心坐标代入直线方程得:-2a-2a+2=0,即a+b=1,
|OA|+|OB|=
+
=(a+b)(
+
)=3+
+
≥3+2
,当且仅当
=
时,取等号.
∴|OA|+|OB|(O为坐标原点)的最小值为3+2
.
故答案为:3+2
.
∵直线l被圆x2+y2+2x-4y+1=0截得的弦长为4,
由直线被圆截取的弦长为4,圆的直径也为4,得到直线过圆心,
把圆心坐标代入直线方程得:-2a-2a+2=0,即a+b=1,
|OA|+|OB|=
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
| 2 |
| b |
| a |
| 2a |
| b |
∴|OA|+|OB|(O为坐标原点)的最小值为3+2
| 2 |
故答案为:3+2
| 2 |
点评:此题考查了直线与圆相交的性质,以及基本不等式,根据题意得到已知直线过圆心是本题的突破点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,若c2-ab=a2+b2,则∠C=( )
| A、60° | B、90° |
| C、120° | D、150° |
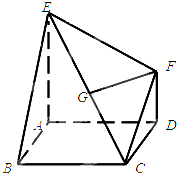 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.