题目内容
现有8个质量和外形一样的球,其中A1,A2,A3为红球的编号,B1,B2,B3为黄球的编号,C1,C2为蓝球的编号,从三种颜色的球中分别选出一个球,放到一个盒子内.
(1)求红球A1被选中的概率;
(2)求黄球B1和蓝球C1不全被选中的概率.
(1)求红球A1被选中的概率;
(2)求黄球B1和蓝球C1不全被选中的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用列举法写出所有基本事件,找出红球A1被选中的基本事件,利用基本事件个数比求概率;
(2)找出黄球B1和蓝球C1不全被选中基本事件,利用基本事件个数比求概率.
(2)找出黄球B1和蓝球C1不全被选中基本事件,利用基本事件个数比求概率.
解答:
解:(1)从三种颜色的球中分别选出一个球,所有基本事件有(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),
(A1,B3,C1),(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),
(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2),
(A3,B3,C1),(A3,B3,C2)共18个.
红球A1被选中的基本事件有6个,
∴红球A1被选中的概率为
;
(2)黄球B1和蓝球C1不全被选中有(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),
(A1,B3,C1),(A1,B3,C2),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),
(A2,B3,C1),(A2,B3,C2),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2),
(A3,B3,C1),(A3,B3,C2)共15个,
∴所求概率为
=
.
(A1,B3,C1),(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),
(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2),
(A3,B3,C1),(A3,B3,C2)共18个.
红球A1被选中的基本事件有6个,
∴红球A1被选中的概率为
| 1 |
| 6 |
(2)黄球B1和蓝球C1不全被选中有(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),
(A1,B3,C1),(A1,B3,C2),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),
(A2,B3,C1),(A2,B3,C2),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2),
(A3,B3,C1),(A3,B3,C2)共15个,
∴所求概率为
| 15 |
| 18 |
| 5 |
| 6 |
点评:本题考查了古典概型的概率计算,利用列举法写出所有基本事件是解答本题的关键.

练习册系列答案
相关题目
 设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(x-6)≥0},B={x|log2(x+2)<4}. 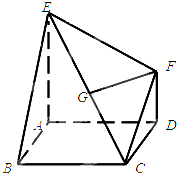 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.