题目内容
 某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.
某高校为了了解参加该校自主招生考试的男女生数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们数学成绩的茎叶图如图所示,其中茎为十位数,叶为个位数.(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该5名女生中随机抽取2名,求至少有一人数学成绩优秀的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(I)根据平均数公式计算可得答案;
(II)利用组合数公式分别计算从5人中任意抽取2名学生的取法种数与至少一名数学成绩在85分以上的取法种数,代入古典概型概率公式计算.
(II)利用组合数公式分别计算从5人中任意抽取2名学生的取法种数与至少一名数学成绩在85分以上的取法种数,代入古典概型概率公式计算.
解答:
解:(Ⅰ)
=
=
=
⇒x=6;
(Ⅱ)女生中85分以上的有2名学生,
从5人中任意抽取2名学生有
=10种方法,
至少有一人数学成绩在85分以上的抽法有
+
×
=7种,
∴至少有一人数学成绩优秀的概率为
.
. |
| x女生 |
| 62+76+84+87+94 |
| 5 |
. |
| x男生 |
| 60+62+64+79+88+80+x+90+91+92+98 |
| 10 |
(Ⅱ)女生中85分以上的有2名学生,
从5人中任意抽取2名学生有
| C | 2 5 |
至少有一人数学成绩在85分以上的抽法有
| C | 2 2 |
| C | 1 2 |
| C | 1 3 |
∴至少有一人数学成绩优秀的概率为
| 7 |
| 10 |
点评:本题考查了由茎叶图求数据的平均数及古典概型的概率计算,熟练掌握茎叶图是解答问题的关键.

练习册系列答案
相关题目
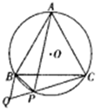 如图,圆O是等边三角形ABC的外接圆,点P在劣弧
如图,圆O是等边三角形ABC的外接圆,点P在劣弧
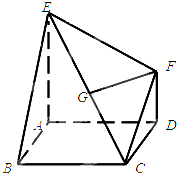 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.