题目内容
已知数列{an}的前n项和为Sn,且满足:Sn=
n2+
n.数列{bn}满足b1=1,2bn-bn-1=0(n≥2,n∈N*).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=anbn,数列{cn}的前n项和为Tn,证明:1≤Tn<4.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=anbn,数列{cn}的前n项和为Tn,证明:1≤Tn<4.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)利用an与sn的关系求得an,由等比数列的定义求得bn;
(Ⅱ)利用错位相减法求得Tn,进行放缩即得结论成立.
(Ⅱ)利用错位相减法求得Tn,进行放缩即得结论成立.
解答:
解:(Ⅰ)当n>1时,an=Sn-Sn-1=n;当n=1时,求得a1=S1=1.
所以an=n.
因为
=
且b1=1,
所以bn=(
)n-1.…(6分)
(Ⅱ)由(Ⅰ),知cn=n•(
)n-1.
所以Tn=1•(
)0+2•(
)1+…+n•(
)n-1,
Tn=1•(
)1+2•(
)2+…+n•(
)n,
于是
Tn=1+(
)1+(
)2+…+(
)n-1-n•(
)n=
-n•(
)n,
化简,得Tn=4-
.
因为
>0,所以Tn<4.
又因为Tn+1-Tn=
>0,所以Tn>Tn-1>…>T1=1.
综上,1≤Tn<4.…(12分)
所以an=n.
因为
| bn |
| bn-1 |
| 1 |
| 2 |
所以bn=(
| 1 |
| 2 |
(Ⅱ)由(Ⅰ),知cn=n•(
| 1 |
| 2 |
所以Tn=1•(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
于是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
1-(
| ||
1-
|
| 1 |
| 2 |
化简,得Tn=4-
| 2n+4 |
| 2n |
因为
| 2n+4 |
| 2n |
又因为Tn+1-Tn=
| n+1 |
| 2n |
综上,1≤Tn<4.…(12分)
点评:本题主要考查了数列通项公式及数列求和的方法,属常规题目,属中档题.

练习册系列答案
相关题目
 某简谐运动的图象对应的函数解析式为:y=
某简谐运动的图象对应的函数解析式为:y=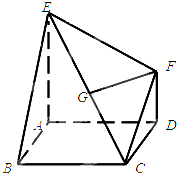 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.