题目内容
已知f(x)=
sinxcosx-cos2x+
.
(1)写出f(x)的最小正周期T;
(2)求由y=f(x)(0≤x≤
),y=0(0≤x≤
),x=
(-1≤y≤0)以及x=0(-
≤y≤0)围成的平面图形的面积.
| 3 |
| 1 |
| 2 |
(1)写出f(x)的最小正周期T;
(2)求由y=f(x)(0≤x≤
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
考点:定积分在求面积中的应用,三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:导数的综合应用,三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式化简整理,利用周期函数求得函数的最小正周期.
(2)利用(1)中f(x)的解析式,运用定积分求得面积.
(2)利用(1)中f(x)的解析式,运用定积分求得面积.
解答:
解:(1)∵f(x)=
sinxcosx-cos2x+
=
sinxcosx-
=
sin2x-
cos2x=sin(2x-
),
∴T=
=π.
(2)设由y=f(x)(0≤x≤
),y=0(0≤x≤
),x=
(-1≤y≤0)以及x=0(-
≤y≤0)围成的平面图形的面积为S,
∵f(x)=sin(2x-
),
∴S=-
sin(2x-
)dx+3
sin(2x-
)dx,
∵[-
]′=sin(2x-
),
∴S=
+3•[
]=2-
.
| 3 |
| 1 |
| 2 |
| 3 |
| 2cos2x-1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
(2)设由y=f(x)(0≤x≤
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
∵f(x)=sin(2x-
| π |
| 6 |
∴S=-
| ∫ |
0 |
| π |
| 6 |
| ∫ |
|
| π |
| 6 |
∵[-
cos(2x-
| ||
| 2 |
| π |
| 6 |
∴S=
cos(2×
| ||||||
| 2 |
cos(2×
| ||||||||
| 2 |
| ||
| 4 |
点评:本题主要考查了三角函数恒等变换的应用,定积分在求面积中的应用,三角函数图象与性质等知识.综合考查了学生分析和推理的能力.

练习册系列答案
相关题目
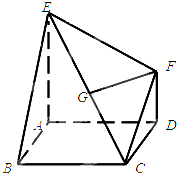 多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.
多面体EABCDF中,底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=1,EA=2.