题目内容
先用求根公式求出方程2x2-3x-1=0的解,然后再借助计算器或计算机,用二分法求出这个方程的近似解(精确度0.1).
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:利用求根公式可得方程2x2-3x-1=0的解x1=
∈(-1,0),x2=
∈(1,2),利用函数零点的判定定理即可得出其估计值.
3-
| ||
| 4 |
3+
| ||
| 4 |
解答:
解:∵方程2x2-3x-1=0的a=2,b=-3,c=-1,
∴x=
,
∵x1=
∈(-1,0),x2=
∈(1,2),
故令f(x)=2x2-3x-1,
由f(-1)=5>0,f(0)=-1<0,⇒x1∈(-1,0);
由f(-0.5)=1>0,⇒x1∈(-0.5,0);
由f(-0.25)=-
<0,⇒x1∈(-0.5,-0.25);
由f(-0.375)=
>0,⇒x1∈(-0.375,-0.25);
由f(-0.3125)=
>0,⇒x1∈(-0.3125,-0.25);
∵|-0.25+0.3125|=0.062 5<0.1,
∴x1≈-0.3,
同理可得x2≈1.8.
∴x=
3±
| ||
| 4 |
∵x1=
3-
| ||
| 4 |
3+
| ||
| 4 |
故令f(x)=2x2-3x-1,
由f(-1)=5>0,f(0)=-1<0,⇒x1∈(-1,0);
由f(-0.5)=1>0,⇒x1∈(-0.5,0);
由f(-0.25)=-
| 13 |
| 8 |
由f(-0.375)=
| 13 |
| 32 |
由f(-0.3125)=
| 17 |
| 128 |
∵|-0.25+0.3125|=0.062 5<0.1,
∴x1≈-0.3,
同理可得x2≈1.8.
点评:熟练掌握函数零点的判定定理及二分法求函数零点的方法、数形结合思想是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
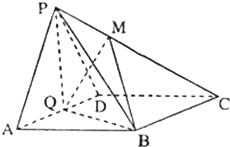 如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,面PAD⊥平面ABCD,PA=PD,Q为AD的中点,且QB⊥AD.
如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,面PAD⊥平面ABCD,PA=PD,Q为AD的中点,且QB⊥AD.