题目内容
已知一个共有n项的等差数列的前4项和为26,末4项和为110,且所有项之和为187,求n的值.
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件得4(a1+an)=26+110=136,解得a1+an=34,从而得到
×34=187,由此能求出的值为11.
| n |
| 2 |
解答:
解:∵一个共有n项的等差数列的前4项和为26,
末4项和为110,且所有项之和为187,
∴4(a1+an)=26+110=136,
解得a1+an=34,
∴
×34=187,
解得n=11.
∴n的值为11.
末4项和为110,且所有项之和为187,
∴4(a1+an)=26+110=136,
解得a1+an=34,
∴
| n |
| 2 |
解得n=11.
∴n的值为11.
点评:本题考查数列的项数的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
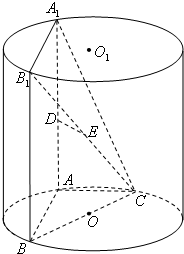 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1,CB1的中点,DE⊥面CBB1.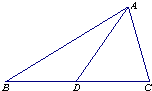 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=