题目内容
已知数列{an}中,an=
,n∈N*,则该数列的前n项和Sn= .
| 2 |
| n(n+1) |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:利用裂项法即可得到结论.
解答:
解:∵an=
=2(
-
),
∴该数列的前n项和Sn=2(1-
+
-
+…+
-
)=2(1-
)=
,
故答案为:
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴该数列的前n项和Sn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
故答案为:
| 2n |
| n+1 |
点评:本题主要考查数列求和,利用裂项法是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
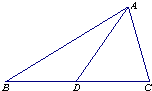 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=