题目内容
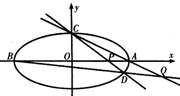 过点C(0,
过点C(0,| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)当直线l过椭圆的右焦点时,求线段CD的长;
(Ⅱ)当点P异于点B时,求证:
| OP |
| OQ |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用过点C(0,
)的椭圆
+
=1(a>b>0)的离心率为
,求出a,b,可得椭圆方程,直线l的方程为y=-
x+
,代入椭圆方程,求出交点坐标,即可求线段CD的长;
(Ⅱ)设直线l的方程为y=kx+
(k≠0且k≠
),代入椭圆方程,求出P,Q的坐标,利用向量的数量积公式,即可得出结论.
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 3 |
(Ⅱ)设直线l的方程为y=kx+
| 3 |
| ||
| 2 |
解答:
 (Ⅰ)解:由已知得b=
(Ⅰ)解:由已知得b=
,
=
,得a=2,
所以,椭圆
+
=1.…(3分)
椭圆的右焦点为F(1,0),
此时直线l的方程为y=-
x+
.
由
解得x1=0,x2=
.
所以|CD|=
|x1-x2|=
×
=
.…(6分)
(Ⅱ)证明:当直线l与x轴垂直时与题意不符,所以直线l与x轴不垂直,即直线的斜率存在.
设直线l的方程为y=kx+
(k≠0且k≠
)…(7分)
代入椭圆的方程,化简得(3+4k2)x2+8
kx=0,解得x1=0或x2=
代入直线l的方程,得y1=
或y2=
.
所以,D的坐标为(
,
).…(9分)
又直线AC的方程为
+
=1,
因为B(-2,0),kBD=
=-
,
所以直线BD的方程为y=-
(x+2).
联立解得
,即Q(-
,2k+
).…(10分)
而P的坐标为P(-
,0),
所以
•
=(-
,0)•(-
,2k+
)=4+0=4.
所以
•
为定值4.…(12分)
 (Ⅰ)解:由已知得b=
(Ⅰ)解:由已知得b=| 3 |
| c |
| a |
| 1 |
| 2 |
所以,椭圆
| x2 |
| 4 |
| y2 |
| 3 |
椭圆的右焦点为F(1,0),
此时直线l的方程为y=-
| 3 |
| 3 |
由
|
解得x1=0,x2=
| 8 |
| 5 |
所以|CD|=
| (1+k2) |
| 4 |
| 8 |
| 5 |
| 16 |
| 5 |
(Ⅱ)证明:当直线l与x轴垂直时与题意不符,所以直线l与x轴不垂直,即直线的斜率存在.
设直线l的方程为y=kx+
| 3 |
| ||
| 2 |
代入椭圆的方程,化简得(3+4k2)x2+8
| 3 |
-8
| ||
| 3+4k2 |
代入直线l的方程,得y1=
| 3 |
| ||
| 3+4k2 |
所以,D的坐标为(
-8
| ||
| 3+4k2 |
| ||
| 3+4k2 |
又直线AC的方程为
| x |
| 2 |
| y | ||
|
因为B(-2,0),kBD=
| y2-0 |
| x2+2 |
| ||
| 2 |
2k+
| ||
2k-
|
所以直线BD的方程为y=-
| ||
| 2 |
2k+
| ||
2k-
|
联立解得
|
| 4k | ||
|
| 3 |
而P的坐标为P(-
| ||
| k |
所以
| OP |
| OQ |
| ||
| k |
| 4k | ||
|
| 3 |
所以
| OP |
| OQ |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量的数量积公式,属于中档题.

练习册系列答案
相关题目
0<x<3是|x-1|<2成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
y=xlnx的导数是( )
| A、x | B、lnx+1 | C、3x | D、1 |
已知F1、F2是双曲线
-
=1的两个焦点,P是此双曲线上的点,∠F1PF2=60°,则△F1PF2的面积等于( )
| x2 |
| 16 |
| y2 |
| 9 |
A、9
| ||
B、8
| ||
C、6
| ||
D、3
|