题目内容
证明:1•3•5•…•
<
.
| 2n-1 |
| 2•4•6•…•2n |
| 2n+1 |
考点:反证法与放缩法
专题:证明题
分析:观察题目,进行一步放缩就可以得出结论.
解答:
证明:
=
•
•
…
≤1<
综上可得
<
| 1•3•5…(2n-1) |
| 2•4•6…2n |
=
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2n-1 |
| 2n |
≤1<
| 2n-1 |
综上可得
| 1•3•5…(2n-1) |
| 2•4•6…2n |
| 2n+1 |
点评:本题主要考察了利用放缩法证明不等式,属于基础题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,以|F1F2|为直径的圆与双曲线渐近线的一个交点为(4,3),则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC中,sinA<sinB是A<B的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
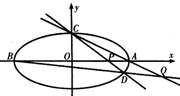 过点C(0,
过点C(0,