题目内容
如图所示,等边三角形OAB的边长为8
,且其三个顶点均在抛物线 C:x2=2py(p>0)上.则抛物线C的方程为 .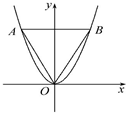
| 3 |

考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知得A(-4
,12),B(4
,12),O(0,0),从而(±4
)2=24p,由此能求出抛物线C的方程.
| 3 |
| 3 |
| 3 |
解答:
解: 如图,∵等边三角形OAB的边长为8
如图,∵等边三角形OAB的边长为8
,
且其三个顶点均在抛物线 C:x2=2py(p>0)上.
∴A(-4
,12),B(4
,12),O(0,0),
∴(±4
)2=24p,
解得p=2.
∴抛物线C的方程为x2=4y.
故答案为:x2=4y.
 如图,∵等边三角形OAB的边长为8
如图,∵等边三角形OAB的边长为8| 3 |
且其三个顶点均在抛物线 C:x2=2py(p>0)上.
∴A(-4
| 3 |
| 3 |
∴(±4
| 3 |
解得p=2.
∴抛物线C的方程为x2=4y.
故答案为:x2=4y.
点评:本题考查抛物线方程的求法,是基础题,解题时要注意待定系数法的合理运用.

练习册系列答案
相关题目
一空间几何体的三视图如图所示,则该几何体的体积为( )


| A、10 | B、20 | C、30 | D、40 |
若等差数列{an}满足a12+a102=10,则S=a10+a11+…+a19的最大值为( )
| A、60 | B、50 | C、45 | D、40 |
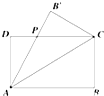 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用,如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P,经试验当△ADP的面积最大时最节能. 如图,在正方体ABCD-A′B′C′D′中,E是棱BC的中点,F是对角线A′C的中点,设
如图,在正方体ABCD-A′B′C′D′中,E是棱BC的中点,F是对角线A′C的中点,设