题目内容

如图，在正方体ABCD-A′B′C′D′中，E是棱BC的中点，F是对角线A′C的中点，设
AB
=
a
，
BC
=
b
，
BB′
=
c
，用
a
，
b
，
c
表示
EF
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：连接A′B，根据已知条件知EF是△A′BC的中位线，所以便可得到
EF
=
1
2
BA′
=
1
2
(-
a
+
c
)．
解答： 解：如图，连接A′B，则EF∥A′B，|EF|=
1
2
|A′B|；
∴
EF
=
1
2
BA′
=
1
2
(-
a
+
c
)．
点评：考查共线向量基本定理，以及向量加法的平行四边形法则．
练习册系列答案
相关题目
两个正数a，b的等差中项是3，一个等比中项是2
2
，且a＞b，则双曲线
x2
b2
-
y2
a2
=1的离心率为
 
．
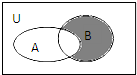设集合U={1，2，3，4，5}，A={2，3，4}，B={3，5}，则图中阴影部分所表示的集合为（　　）
A、{2，3}B、{1，4}
C、{5}D、{6}
为选拔选手参加“中国汉字听写大会”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在[50，60），[90，100]的数据）．
（1）求样本容量n和频率分布直方图中的x、y的值；
（理科）（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取3名学生参加“中国汉字听写大会”，设随机变量X表示所抽取的3名学生中得分在[80，90，）内的学生人数，求随机变量X的分布列及数学期望．
（文科）（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取2名学生参加“中国汉字听写大会”，求所抽取的2名学生中至少有一人得分在[90，100]内的概率．
如图所示，等边三角形OAB的边长为8
3
，且其三个顶点均在抛物线 C：x2=2py（p＞0）上．则抛物线C的方程为
 
．
设A，B为抛物线y2=2px（p＞0）上不同的两点，O为坐标原点，且OA⊥OB，则△OAB面积的最小值为（　　）
A、p2
B、2p2
C、4p2
D、6p2
执行如图所示的程序框图，则输出的z的值是
 
．
给出命题：已知实数a、b满足a+b=1，则ab≤
1
4
．它的逆命题、否命题、逆否命题三个命题中，真命题的个数是
 
．
在△ABC中，角A，B，C的对边分别为a，b，c，已知bcosC+
3
bsinC-a-c=0．
（Ⅰ）求B；
（Ⅱ）若b=
3
，求2a+c的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网