题目内容
在以下结论中,
①对随机事件A,B,都有P(A+B)=P(A)+P(B);
②若1<m<3,则方程
+
=1表示椭圆;
③若直线y+(m2-2)x+1=0与直线y-x+m=0有公共点,则m≠-1;
④平面内,到两定点的距离的差的绝对值为常数的点的轨迹是双曲线;
⑤已知圆M:(x+cosθ)2+(y-sinθ)2=1,直线l:y=kx,则对任意实数k与θ,直线l和圆M有公共点;
正确的结论序号是 .
①对随机事件A,B,都有P(A+B)=P(A)+P(B);
②若1<m<3,则方程
| x2 |
| m-1 |
| y2 |
| 3-m |
③若直线y+(m2-2)x+1=0与直线y-x+m=0有公共点,则m≠-1;
④平面内,到两定点的距离的差的绝对值为常数的点的轨迹是双曲线;
⑤已知圆M:(x+cosθ)2+(y-sinθ)2=1,直线l:y=kx,则对任意实数k与θ,直线l和圆M有公共点;
正确的结论序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:由相互独立事件的概率乘法公式说明①错误;距离说明②错误;由两直线有公共点的条件求出m的范围说明③正确;
距离说明④错误;由圆和直线都过原点说明④正确.
距离说明④错误;由圆和直线都过原点说明④正确.
解答:
解:对于①,若随机事件A,B相互独立,则P(A+B)=P(A)P(B),命题①错误;
对于②,若1<m<3,则方程
+
=1表示椭圆错误,如m=2时表示圆;
对于③,若直线y+(m2-2)x+1=0与直线y-x+m=0有公共点,则
或m2-2≠-1,
∴m≠-1.命题③正确;
对于④,平面内,到两定点的距离的差的绝对值为常数的点的轨迹是双曲线错误,若到两定点的距离的差的绝对值等于两定点的距离则表示两条射线;
对于⑤,圆M:(x+cosθ)2+(y-sinθ)2=1的圆心为(-cosθ,sinθ),半径为1,
∴圆M过原点,而直线y=kx过原点,则对任意实数k与θ,直线l和圆M有公共点,命题⑤正确.
故答案为:③⑤.
对于②,若1<m<3,则方程
| x2 |
| m-1 |
| y2 |
| 3-m |
对于③,若直线y+(m2-2)x+1=0与直线y-x+m=0有公共点,则
|
∴m≠-1.命题③正确;
对于④,平面内,到两定点的距离的差的绝对值为常数的点的轨迹是双曲线错误,若到两定点的距离的差的绝对值等于两定点的距离则表示两条射线;
对于⑤,圆M:(x+cosθ)2+(y-sinθ)2=1的圆心为(-cosθ,sinθ),半径为1,
∴圆M过原点,而直线y=kx过原点,则对任意实数k与θ,直线l和圆M有公共点,命题⑤正确.
故答案为:③⑤.
点评:本题考查了命题的真假判断与应用,考查了直线与圆位置关系的判断,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
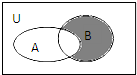 设集合U={1,2,3,4,5},A={2,3,4},B={3,5},则图中阴影部分所表示的集合为( )
设集合U={1,2,3,4,5},A={2,3,4},B={3,5},则图中阴影部分所表示的集合为( )| A、{2,3} | B、{1,4} |
| C、{5} | D、{6} |