题目内容
1.已知圆B的圆心B坐标为(2,1)直线l:x+2y-2=0与圆B相交于M,N两点,|MN|=$\frac{2\sqrt{5}}{5}$.(1)求圆B的方程;
(2)设直线l:x+2y-2=0与x,y轴分别交于点A,C,将四边形OABC折叠,使O点落在线段CB上,若折痕所在直线的斜率为k,试写出折痕所在直线的方程.
分析 (1)设圆的半径为r,运用点到直线的距离公式和弦长公式,计算可得r=1,进而得到圆的方程;
(2)由题意可得四边形OABC为矩形,即可得到对称轴的斜率,即可得到所求直线方程.
解答 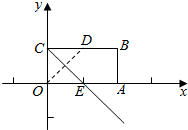 解:(1)设圆的半径为r,
解:(1)设圆的半径为r,
圆心到直线的距离为d=$\frac{|2+2-2|}{\sqrt{1+4}}$=$\frac{2}{\sqrt{5}}$,
可得弦长为|MN|=2$\sqrt{{r}^{2}-\frac{4}{5}}$=$\frac{2\sqrt{5}}{5}$,
解得r=1,
即有圆B的方程为(x-2)2+(y-1)2=1;
(2)由题意可得A(2,0),C(0,1),
四边形OABC为矩形,
设O点与D点关于直线CE对称,
可得直线CE的斜率为-1,
即有直线CE的方程为y=-x+1,
即折痕所在直线的方程为y=-x+1.
点评 本题考查圆的方程的求法,注意运用点到直线的距离公式和弦长公式,考查对称问题的解法,注意结合图形,考查运算能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
11.下面四个条件中,使a>b成立的充要条件是( )
| A. | |a|>|b| | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | a2>b2 | D. | 2a>2b |
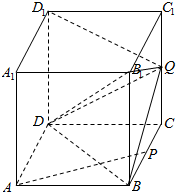 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.