Question

如图（1）已知矩形ABCD中，AD=4，E、F分别是AD、BC的中点，点O在EF上，且FO=3OE，把△ABE沿着BE翻折，使点A在平面BCD上的射影恰为点O（如图（2））．

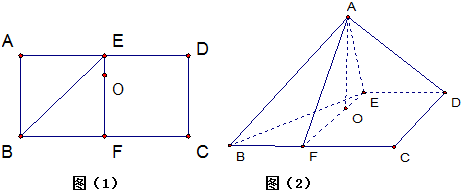
（1）求证：平面ABF⊥平面AEF；
（2）求二面角E-AB-F的大小．

Answer 1

考点：二面角的平面角及求法,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）由已知得EF⊥BF，AO⊥平面BCD，从而BF⊥AO，进而BF⊥平面AEF，由此能证明平面ABF⊥平面AEF．
（2）设DC=t，则OE=

t

4

，OF=

3

4

t，AE=BF=2，AO⊥EF，AO=

4- t2 16

=

64-t2 16

，过O作OG∥BC，交BE于G，则OG=

1

2

，AG=

t2+36

4

，从而求出t=4，以D为原点，DE为x轴，DC为y轴，建立空间直角坐标系，利用向量法能求出二面角E-AB-F的大小．

解答： （1）证明：∵矩形ABCD中，AD=4，E、F分别是AD、BC的中点，
∴EF⊥BF，把△ABE沿着BE翻折后，仍有EF⊥BF，
∵把△ABE沿着BE翻折，使点A在平面BCD上的射影恰为点O，
∴AO⊥平面BCD，又BF?平面BCD，
∴BF⊥AO，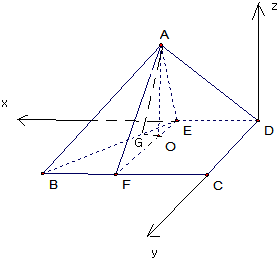
∵EF∩AO=O，
∴BF⊥平面AEF，
∵BF?平面ABF，∴平面ABF⊥平面AEF．
（2）解：设DC=t，则OE=

t

4

，OF=

3

4

t，AE=BF=2，AO⊥EF，
∴AO=

4- t2 16

=

64-t2 16

，
过O作OG∥BC，交BE于G，则OG=

1

2

，AG=

t2+36

4

，
∴AO=

t2+36 16 - 1 4

，从而

t2+36

16

-

1

4

=4-

t2

16

，解得t=4，或t=-4（舍），
∴AO=

3

，
以D为原点，DE为x轴，DC为y轴，建立空间直角坐标系，
则D（0，0，0），E（2，0，0），F（2，4，0），A（2，1，

3

），B（4，4，0），

AE

=(0，-1，-

3

)，

AB

=（2，3，-

3

），

BF

=（-2，0，0），

AF

=(0，2，-

3

)，
设平面AEB的法向量为

n

=（x，y，z），
则

n • AB =2x+3y- 3 z=0 n • AE =-y- 3 z=0

，取z=

3

，得

n

=(6，-3，

3

)，
设平面ABF的法向量为

m

=(a，b，c)，
则

m • AB =2a+3b- 3 c=0 m • AF =2b- 3 c=0

，取c=

3

，得

m

=（-3，6，4

3

），
|cos＜

m

，

n

＞|=|

-18-18+12

36+9+3 • 9+36+48

|=

2 31

31

．
∴二面角E-AB-F的大小为arccos

2 31

31

．

点评：本题考查平面与平面垂直的证明，考查二面角的大小的求法，解题时要认真审题，注意向量法的合理运用．