题目内容
某流程图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
A、f（x）=
| ||||
B、f（x）=ln（
| ||||
C、f（x）=
| ||||
D、f（x）=
|
考点：程序框图
专题：计算题,图表型
分析：本题的框图是一个选择结构，其算法是找出即是奇函数存在零点的函数，由此规则对四个选项进行比对，即可得出正确选项．
解答：
解：由框图知，其算法是输出出即是奇函数存在零点的函数，
A中，函数f（x）=
不能输出，因为此函数没有零点；A不正确．
B中，函数f（x）=ln（
-x）可以输出，∵f（-x）=lg（+x）=-f（x）发现，函数是奇函数且当x=0时函数值为0，故B正确；
C中，函数f（x）=
，不能输出，因为不存在零点；C不正确．
D中，函数f（x）=
，不能输出，因为它是偶函数，不是奇函数，D不正确．
故选B．
A中，函数f（x）=
| |x| |
| x |
B中，函数f（x）=ln（
| x2+1 |
C中，函数f（x）=
| ex+e-x |
| ex-e-x |
D中，函数f（x）=
| ||
| |x+3|+|4-x| |
故选B．
点评：本题考查选择结构，解答本题的关键是根据框图得出函数所满足的性质，然后比对四个选项中的函数，对四个函数的性质比较了解也是判断出正确答案的关键．
练习册系列答案
相关题目
已知函数y=f（x）和y=g（x）的图象如图，则有（ ）
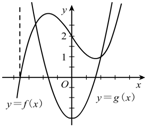
| A、f′（x）=g（x） |
| B、g′（x）=f（x） |
| C、f′（x）=g′（x） |
| D、g（x）=f（x） |
已知直线l：x+my+4=0，若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称，则m的值为（ ）
| A、2 | B、-2 | C、1 | D、-1 |
已知盒中有10个灯泡，其中8个正品，2个次品．需要从中取出2个正品，每次取出1个，取出后不放回，直到取出2个正品为止．设ξ为取出的次数，求P（ξ=4）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
与-525°的终边相同的角可表示为（ ）
| A、525°-k•360°（k∈Z） |
| B、165°+k•360°（k∈Z） |
| C、195°+k•360°（k∈Z） |
| D、-195°+k•360°（k∈Z） |
已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与B的距离为（ ）
A、
| ||
| B、a km | ||
C、
| ||
| D、2a km |
函数y=
的定义域是（ ）
| ||
| tanx |
A、{x|2kπ≤x≤2kπ+
| ||||
B、{x|2kπ＜x＜2kπ+
| ||||
| C、{x|2kπ＜x＜2kπ+π，k∈Z} | ||||
D、{x|2kπ-
|
设集合M={0，1}，N={x∈Z|y=
}，则（ ）
| x+1 |
| A、M∩N=∅ |
| B、M∩N={0} |
| C、M∩N={1} |
| D、M∩N=M |
