题目内容
设等差数列{an}的前n项和为Sn,已知a3=3,S11=0.
(1)求数列{an}的通项公式;
(2)当n为何值时,Sn最大,并求Sn的最大值.
(1)求数列{an}的通项公式;
(2)当n为何值时,Sn最大,并求Sn的最大值.
考点:等差数列的性质
专题:等差数列与等比数列
分析:(1)由题意可得得a6=2,进而求出公差d,代入可得{an}的通项公式;
(2)求出前n项和为Sn的表达式,进而根据二次函数的图象和性质得到Sn的最大值.
(2)求出前n项和为Sn的表达式,进而根据二次函数的图象和性质得到Sn的最大值.
解答:
解:(1)由等差数列的求和公式和性质可得:
S11=11×a6=0,
解得a6=2,
又∵a3=3,
故数列{an}的公差d=-1,
故an=a3+(n-3)×-1=6-n;
(2)由(1)得a1=5,
故Sn=a1n+
d=-
n2+
n,
故当n=5,或6时,Sn最大,
Sn的最大值为15
S11=11×a6=0,
解得a6=2,
又∵a3=3,
故数列{an}的公差d=-1,
故an=a3+(n-3)×-1=6-n;
(2)由(1)得a1=5,
故Sn=a1n+
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 11 |
| 2 |
故当n=5,或6时,Sn最大,
Sn的最大值为15
点评:本题考查的知识点是等差数列的性质,等差数列{an}的前n项和,二次函数的图象和性质,难度不大,属于基础题.

练习册系列答案
相关题目
若a>0,b>0,a+b=2,给出下列四个结论:①ab≤1②
+
≤
③a2+b2≥2④
+
≥2,其中所有正确结论的序号是( )
| a |
| b |
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、①② | B、②③④ |
| C、③④ | D、①③④ |
下列函数f(x)中,在(0,+∞)上是减函数的是( )
A、f(x)=
| ||
| B、f(x)=x3 | ||
| C、f(x)=lnx | ||
| D、f(x)=2x |
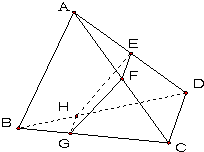 如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,
如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,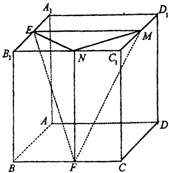 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.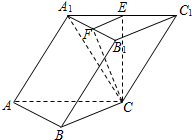 在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.
在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.