题目内容
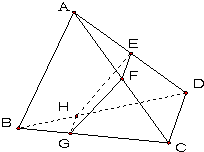 如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,
如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:
(1)HG∥平面ACD;
(2)CD∥EF.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由平行四边形EFGH,得HG∥EF,由此能证明HG∥平面ACD.
(2)HG∥平面ACD,HG∥EF,平面ACD∩平面ACD=CD,由此能证明CD∥EF.
(2)HG∥平面ACD,HG∥EF,平面ACD∩平面ACD=CD,由此能证明CD∥EF.
解答:
(本题满分8分)
证明:(1)∵平行四边形EFGH,
∴HG∥EF,
∵HG?平面ACD
EF?平面ACD,
∴HG∥平面ACD;….(4分)
(2)∵HG∥平面ACD
HG?平面BCD,HG∥EF,
平面ACD∩平面ACD=CD
∴CD∥EF….(8分)
证明:(1)∵平行四边形EFGH,
∴HG∥EF,
∵HG?平面ACD
EF?平面ACD,
∴HG∥平面ACD;….(4分)
(2)∵HG∥平面ACD
HG?平面BCD,HG∥EF,
平面ACD∩平面ACD=CD
∴CD∥EF….(8分)
点评:本题考查直线与平面平行的证明,考查直线与直线与平行的证明,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
函数f(x)=x3-8,g(x)=3x-1,则不等式f[g(x)]≥0的解集是( )
| A、[1,+∞) |
| B、[ln3,+∞) |
| C、[1,ln3] |
| D、[log32,+∞) |
在△ABC中,∠C=90°,CD是斜边AB上的高.已知CD=
,BC=
,则AD=( )
| 2 |
| 6 |
| A、1 | B、2 | C、3 | D、4 |
等差数列{an}中,a1=1,d=1,则该数列的前n项和Sn=( )
| A、n | ||
| B、n(n+1) | ||
| C、n(n-1) | ||
D、
|
 在△ABC中,已知AB=2,AC=2
在△ABC中,已知AB=2,AC=2