题目内容
设数列{an}的前n项和Sn=n2+2n（n∈N*）．
（1）写出数列的前三项a1，a2，a3；
（2）求通项an．
（1）写出数列的前三项a1，a2，a3；
（2）求通项an．
考点：等差数列的性质,等差数列的通项公式
专题：等差数列与等比数列
分析：（1）通过你=1，2，3，分别求出数列的前三项a1，a2，a3；
（2）利用an=Sn-Sn-1，即可求出数列的通项公式．
（2）利用an=Sn-Sn-1，即可求出数列的通项公式．
解答：
解：（1）a1=S1=12+2=3，
a2=22+2×2-3=5；
a3=S3-S2=7．
（2）n∈N*．n≥2，an=Sn-Sn-1=2n+1，
又n=1时a1=S1=3，∴an=2n+1．
a2=22+2×2-3=5；
a3=S3-S2=7．
（2）n∈N*．n≥2，an=Sn-Sn-1=2n+1，
又n=1时a1=S1=3，∴an=2n+1．
点评：本题考查数列的通项公式的求法，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
若ξ～B（10，
），则p（ξ≥2）等于（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a，b为非零实数，且a＞b，则下列不等式成立的是（ ）
| A、a2b＞ab2 | ||||
| B、a2＞b2 | ||||
C、
| ||||
D、
|
等差数列{an}中，a1=1，d=1，则该数列的前n项和Sn=（ ）
| A、n | ||
| B、n（n+1） | ||
| C、n（n-1） | ||
D、
|
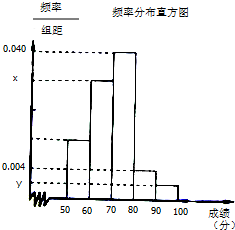某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成的频率分布表和频率分布直方图（如图所示）解决下列问题：