题目内容
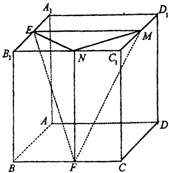 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.(Ⅰ)用向量方法求直线EF与MN的夹角;
(Ⅱ)求二面角N-EF-M的平面角的正切值.
考点:二面角的平面角及求法,异面直线
专题:空间向量及应用
分析:(Ⅰ)建立空间直角坐标系利用向量方法求直线EF与MN的夹角;
(Ⅱ)求出两个平面的法向量,根据法向量之间的关系,即可求二面角N-EF-M的平面角的正切值.
(Ⅱ)求出两个平面的法向量,根据法向量之间的关系,即可求二面角N-EF-M的平面角的正切值.
解答:
解:(Ⅰ)以A为坐标原点,建立空间直角坐标系如图:
设正方体的棱长为1,
则A(0,0,0),B(1,0,0),E(
,0,1),F(1,
,0),
M(
,1,1),N(1,
,1),
则
=(
,
,-1),
=(
,-
,0),
则
•
=(
,
,-1)•(
,-
,0)=
×
-
×
+0=0,
则
⊥
,
即直线EF与MN的夹角为90°;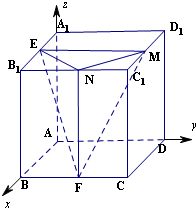
(Ⅱ)∵直线EF与MN的夹角为90°,
∴EF⊥MN,
∵FN⊥MN,MN∩FN=N,
∴MN⊥平面ENF,
即向量
=(
,-
,0)是平面ENF的法向量,
设平面EFM的法向量为
=(x,y,z),
则
=(0,1,0),
=(
,
,-1),
则
,
即y=0,x=2z,设z=1,则x=2,即
=(2,0,1),
则cos<
,
>=
=
=
,
则sin<
,
>=
=
=
=
,
则tan<
,
>=
=
=
.
设正方体的棱长为1,
则A(0,0,0),B(1,0,0),E(
| 1 |
| 2 |
| 1 |
| 2 |
M(
| 1 |
| 2 |
| 1 |
| 2 |
则
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
则
| EF |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则
| EF |
| EF |
即直线EF与MN的夹角为90°;

(Ⅱ)∵直线EF与MN的夹角为90°,
∴EF⊥MN,
∵FN⊥MN,MN∩FN=N,
∴MN⊥平面ENF,
即向量
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
设平面EFM的法向量为
| n |
则
| EM |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
则
|
即y=0,x=2z,设z=1,则x=2,即
| n |
则cos<
| n |
| MN |
| ||||
|
|
| 1 | ||||||
|
| ||
|
则sin<
| n |
| MN |
1-(
|
1-
|
|
| ||
|
则tan<
| n |
| MN |
| ||||||
|
| ||
|
| ||
| 2 |
点评:本题主要考查二面角的求解以及利用向量法求解异面直线的角的大小运算量较大.

练习册系列答案
相关题目
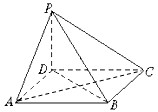 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD. 如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2