题目内容
已知{an}是首项a1=2且公比q≠1的等比数列,a1,2a2,3a3依次成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{an}的前n项和为Sn,若不等式
>λ对任意n∈N*恒成立,求实数λ的范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{an}的前n项和为Sn,若不等式
| Sn-1 |
| Sn+1-1 |
考点:数列的求和,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)设出公比利用已知等差关系,以及等比数列通项公式,求出公比,即可求数列{an}的通项公式;
(Ⅱ)求出数列{an}的前n项和为Sn,求出
的最小值,即可求实数λ的范围.
(Ⅱ)求出数列{an}的前n项和为Sn,求出
| Sn-1 |
| Sn+1-1 |
解答:
解:(Ⅰ) 由题,设{an}的公比为q,则an=2qn-1,
由a1,2a2,3a3依次成等差数列,所以4a2=2+3a3. …(2分)
即8q=2+6q2,解得q=1或q=
又q≠1,故q=
…(4分)
所以数列{an}的通项公式为an=
. …(6分)
(Ⅱ)由(Ⅰ)得,an=
,所以Sn=
=3(1-
) …(8分)
则
=
=
=1-
,
∵2×3n-1≥5,∴1-
∈[
,1)…(11分)
由
>λ恒成立,得λ<
. …(13分)
由a1,2a2,3a3依次成等差数列,所以4a2=2+3a3. …(2分)
即8q=2+6q2,解得q=1或q=
| 1 |
| 3 |
| 1 |
| 3 |
所以数列{an}的通项公式为an=
| 2 |
| 3n-1 |
(Ⅱ)由(Ⅰ)得,an=
| 2 |
| 3n-1 |
2(1-
| ||
1-
|
| 1 |
| 3n |
则
| Sn-1 |
| Sn+1-1 |
2-
| ||
2-
|
| 2×3n-1-3 |
| 2×3n-1 |
| 2 |
| 2×3n-1 |
∵2×3n-1≥5,∴1-
| 2 |
| 2×3n-1 |
| 3 |
| 5 |
由
| Sn-1 |
| Sn+1-1 |
| 3 |
| 5 |
点评:本题考查等差数列以及等比数列的综合应用,数列求和以及函数恒成立关系,考查计算能力、转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆的中心在原点,焦点在x轴上,长轴长为4,过焦点且垂直于长轴的弦长为3,则椭圆的方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}中,a1=1,d=1,则该数列的前n项和Sn=( )
| A、n | ||
| B、n(n+1) | ||
| C、n(n-1) | ||
D、
|
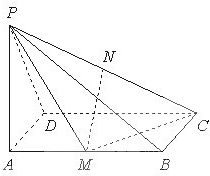 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.