题目内容
9．设等比数列{an}的前n项和为Sn，S4=1，S8=17，则首项a1=$\frac{1}{15}$或-$\frac{1}{5}$．分析 由等比数列前n项和公式列出方程组，由此能求出首项．
解答 解：∵等比数列{an}的前n项和为Sn，S4=1，S8=17，
∴$\left\{\begin{array}{l}{{S}_{4}=\frac{{a}_{1}（1-{q}^{4}）}{1-q}=1}\\{{S}_{8}=\frac{{a}_{1}（1-{q}^{8}）}{1-q}=17}\end{array}\right.$，
解得${a}_{1}=-\frac{1}{5}$，q=-2或${a}_{1}=\frac{1}{15}$，q=2，
∴首项a1为$\frac{1}{15}或-\frac{1}{5}$．
故答案为：$\frac{1}{15}或-\frac{1}{5}$．
点评 本题考查等比数列的首项的求法，是中档题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
相关题目
20．设函数f（x）是定义在R上的偶函数，f'（x）为其导函数．当x＞0时，f（x）+x•f′（x）＞0，且f（1）=0，则不等式x•f（x）＞0的解集为（ ）
| A． | （-∞，-1）∪（1，+∞） | B． | （-∞，-1）∪（0，1） | C． | （-1，0）∪（0，1） | D． | （-1，0）∪（1，+∞） |
4．
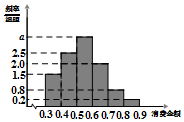某电商对10000名网购者2015年度消费情况进行统计，其消费频率分布直方图如图，则在这些网购者中，消费金额在[0.5，0.9]内的人数为（ ）
某电商对10000名网购者2015年度消费情况进行统计，其消费频率分布直方图如图，则在这些网购者中，消费金额在[0.5，0.9]内的人数为（ ）| A． | 2000 | B． | 4500 | C． | 6000 | D． | 7500 |
18．
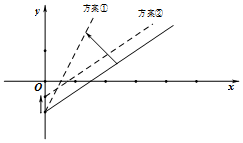如图是某条公共汽车线路收支差额y与乘客量x的图象（实线），由于目前本线路亏损，公司有关人员提出两种扭亏为盈的方案（虚线），这两种方案分别是（ ）
如图是某条公共汽车线路收支差额y与乘客量x的图象（实线），由于目前本线路亏损，公司有关人员提出两种扭亏为盈的方案（虚线），这两种方案分别是（ ）| A． | 方案①降低成本，票价不变，方案②提高票价而成本不变； | |
| B． | 方案①提高票价而成本不变，方案②降低成本，票价不变； | |
| C． | 方案①降低成本，票价提高，方案②提高票价而成本不变； | |
| D． | 方案①提高成本，票价不变，方案②降低票价且成本降低 |