题目内容
已知函数f(x)=loga(1-ax)(a>0,a≠1).
(1)求f(x)的定义域;
(2)当a>1时,判断函数f(x)的单调性,并证明你的结论.
(1)求f(x)的定义域;
(2)当a>1时,判断函数f(x)的单调性,并证明你的结论.
考点:对数函数的图像与性质
专题:计算题,证明题,函数的性质及应用
分析:(1)由题意得,1-ax>0;从而讨论a以求函数的定义域;
(2)当a>1时,函数f(x)在其定义域(-∞,0)上是减函数,利用定义法证明.
(2)当a>1时,函数f(x)在其定义域(-∞,0)上是减函数,利用定义法证明.
解答:
解:(1)由题意得,1-ax>0;
当0<a<1时,1-ax>0的解集为(0,+∞);
故f(x)的定义域为(0,+∞);
当a>1时,1-ax>0的解集为(-∞,0);
故f(x)的定义域为(-∞,0);
(2)当a>1时,函数f(x)在其定义域(-∞,0)上是减函数,
证明如下,
任取x1,x2∈(-∞,0),且x1<x2,
∵a>1,则ax1<ax2;
故1-ax1>1-ax2;
故loga(1-ax1)>loga(1-ax2);
故f(x1)>f(x2);
故函数f(x)在其定义域(-∞,0)上是减函数.
当0<a<1时,1-ax>0的解集为(0,+∞);
故f(x)的定义域为(0,+∞);
当a>1时,1-ax>0的解集为(-∞,0);
故f(x)的定义域为(-∞,0);
(2)当a>1时,函数f(x)在其定义域(-∞,0)上是减函数,
证明如下,
任取x1,x2∈(-∞,0),且x1<x2,
∵a>1,则ax1<ax2;
故1-ax1>1-ax2;
故loga(1-ax1)>loga(1-ax2);
故f(x1)>f(x2);
故函数f(x)在其定义域(-∞,0)上是减函数.
点评:本题考查了函数的定义域的求法及函数的单调性的证明,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
函数f(x)=Asin(2x+Φ)(A>0,Φ∈R)的部分图象如图所示,则f(-
)=( )
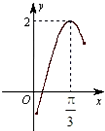
| π |
| 24 |

| A、-1 | ||||
B、-
| ||||
C、-
| ||||
D、-
|
设等差数列{an}的前n项和为Sn,若a11-a8=3,则使S11-S8=3,最小正整数an>0的值是( )
| A、8 | B、9 | C、11 | D、10 |
在命题“方程x2=4的解是x=±2”中,逻辑联结词的使用情况是( )
| A、使用了逻辑联结词“或” |
| B、使用了逻辑联结词“且” |
| C、使用了逻辑联结词“非” |
| D、未使用逻辑联结词“或”、“且”、“非” |