Question

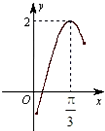
函数f（x）=Asin（2x+Φ）（A＞0，Φ∈R）的部分图象如图所示，则f（-

π

24

）=（　　）

• A、-1
• B、-

  1

  2

• C、-

  3

  2

• D、-

  2

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：计算题,三角函数的求值

分析：由图可知，A=2，f（

π

3

）=2，可得2sin（

2π

3

+φ）=2，即解得φ的值，从而求出解析式，即可求f（-

π

24

）=2sin（-

π

12

-

π

6

）的值．

解答： 解：由图可知，A=2，f（

π

3

）=2，
∴2sin（

2π

3

+φ）=2，即sin（

2π

3

+φ）=1，
∴解得：

2π

3

+φ=

π

2

+2π（k∈Z），
∴解得：φ=-

π

6

+2kπ，（k∈Z），
∴f（x）=2sin（2x-

π

6

+2kπ）=2sin（2x-

π

6

）．
∴f（-

π

24

）=2sin（-

π

12

-

π

6

）=2sin（-

π

4

）=-

2

．
故选：D．

点评：本题主要考察了由y=Asin（ωx+φ）的部分图象确定其解析式，三角函数求值，属于基础题．