题目内容
20.已知函数$f(x)=\frac{x}{{{e^{sin({x-\frac{π}{2}})}}}}$(e为自然对数的底数),当x∈[-π,π]时,y=f(x)的图象大致是( )| A. |  | B. | 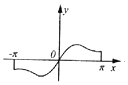 | C. | 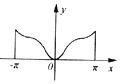 | D. | 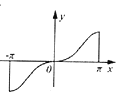 |
分析 利用函数的奇偶性以及函数的特殊值判断即可.
解答 解:函数$f(x)=\frac{x}{{{e^{sin({x-\frac{π}{2}})}}}}$=$\frac{x}{{e}^{-cosx}}$,
f(-x)=-$\frac{x}{{e}^{-cosx}}$=-f(x),函数是奇函数,排除选项A,C,
当x=π时,f(π)=$\frac{π}{e}$>1,
排除B,
故选:D.
点评 本题考查函数的图象的判断,函数奇偶性以及特殊值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知非零向量$\overrightarrow m$,$\overrightarrow n$满足|$\overrightarrow m|=2|\overrightarrow n|$,cos<$\overrightarrow m,\overrightarrow n>=\frac{1}{3}$,若$\overrightarrow m⊥(t\overrightarrow n+\overrightarrow m)$,则实数t的值为( )
| A. | -6 | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
8.已知直线a⊥平面α,则“直线b∥平面α”是“直线a⊥直线b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF. 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD. 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED=$\sqrt{3}$.M为棱FC上一点,平面ADM与棱FB交于点N.