题目内容
已知f（x）=3x2-x+4，f[g（x）]=3x4+18x3+50x2+69x+48，那么整系数多项式函数g（x）的各项系数和为（ ）
| A、8 | B、9 | C、10 | D、11 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：先设出g（x）的表达式，将g（x）代入f（x），利用系数相等，求出g（x）的系数，从而得到答案．
解答：
解：由题意得g（x）的表达式是二次式，
设g（x）=ax2+bx+c，
∴f[g（x）]=3（ax2+bx+c）2-（ax2+bx+c）+4
=3a2x4+6abx3+（3b2+6ac-a2）x2+（6bc-b）x+3c2-c+4
=3x4+18x3+50x2+69x+48，
∴
，解得：
，
∴a+b+c=8，
故选：A．
设g（x）=ax2+bx+c，
∴f[g（x）]=3（ax2+bx+c）2-（ax2+bx+c）+4
=3a2x4+6abx3+（3b2+6ac-a2）x2+（6bc-b）x+3c2-c+4
=3x4+18x3+50x2+69x+48，
∴
|
|
∴a+b+c=8，
故选：A．
点评：本题考查了求函数的解析式问题，待定系数法是常用的方法之一，必要属于基础题．
练习册系列答案
相关题目
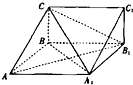如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，∠A1AB=45°，四边形BCC1B1为矩形，若AC=5，AB=4，BC=3．
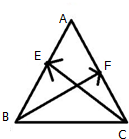如图，在边长为2的正△ABC中，E、F分别是AB、AC的中点，求下列说法正确的是（ ）
| A、若p∧q为假命题，则p、q都为假命题 | ||||||||
| B、“f（0）=0”是“函数f（x）为奇函数”充要条件 | ||||||||
| C、若命题p：?x0∈R，2x02+x0+3＞0，则?p：?x∈R，2x2+x+3＜0 | ||||||||
D、若“a=
|