题目内容
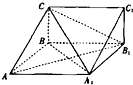 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.(1)求证:AB1⊥平面A1BC;
(2)求三棱锥C-A1B1C1的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知得BC⊥AB,CB⊥BB1,从而CB⊥平面AA1B1B,进而CB⊥AB1,又AB1⊥A1B,由此能证明AB1⊥平面A1BC.
(2)过B作BD⊥A1B1于D,由已知得BD⊥平面A1B1C1,由此能求出三棱锥C-A1B1C1的体积.
(2)过B作BD⊥A1B1于D,由已知得BD⊥平面A1B1C1,由此能求出三棱锥C-A1B1C1的体积.
解答:
(1)证明:在△ABC中,AC=5,AB=4,BC=3,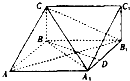
满足AC2=AB2+BC2,
∴∠ABC=90°,∴BC⊥AB,
又∵四边形BCC1B1为矩形,∴CB⊥BB1,
又BB1?平面AA1B1B,AB?平面AA1B1B,BB1∩AB=B,
∴CB⊥平面AA1B1B,
又∵AB1?平面AA1B1B,∴CB⊥AB1,
又∵四边形A1ABB1为菱形,∴AB1⊥A1B,
又CB?平面AA1B1B,A1B?平面A1BC,CB∩A1B=B,
∴AB1⊥平面A1BC.
(2)解:过B作BD⊥A1B1于D,
由(1)得CB⊥平面AA1B1B,
∴C1B1⊥平面AA1B1B,∴C1B1⊥BD,
∴BD⊥平面A1B1C1,
∵四边形A1ABB1为菱形,∠A1AB=45°,
∴2BD2=16,解得BD=2
,
V C-A1B1C1=
×
A1B1•B1C1•BD=
×
×4×3×2
=4
,
∴三棱锥C-A1B1C1的体积为4
.

满足AC2=AB2+BC2,
∴∠ABC=90°,∴BC⊥AB,
又∵四边形BCC1B1为矩形,∴CB⊥BB1,
又BB1?平面AA1B1B,AB?平面AA1B1B,BB1∩AB=B,
∴CB⊥平面AA1B1B,
又∵AB1?平面AA1B1B,∴CB⊥AB1,
又∵四边形A1ABB1为菱形,∴AB1⊥A1B,
又CB?平面AA1B1B,A1B?平面A1BC,CB∩A1B=B,
∴AB1⊥平面A1BC.
(2)解:过B作BD⊥A1B1于D,
由(1)得CB⊥平面AA1B1B,
∴C1B1⊥平面AA1B1B,∴C1B1⊥BD,
∴BD⊥平面A1B1C1,
∵四边形A1ABB1为菱形,∠A1AB=45°,
∴2BD2=16,解得BD=2
| 2 |
V C-A1B1C1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
∴三棱锥C-A1B1C1的体积为4
| 2 |
点评:本题考查直线与平面垂直的证明,考查三棱锥的体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列函数中是奇函数是( )
A、y=x3-x+
| ||||||
B、y=
| ||||||
| C、y=x4-x2 | ||||||
| D、y=x6+x2+2 |
函数y=|cosx|的最小正周期是( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
某同学通过计算机测试的概率为
,他连续测试3次,其中恰有1次通过的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知椭圆E:
已知椭圆E: