题目内容
在正方体ABCD-A1B1C1D1中,M,N,F分别是AA1,BB1,BC的中点.
(1)求证:D1N垂直B1F;
(2)求直线CM与D1N所成角的余弦值.
(1)求证:D1N垂直B1F;
(2)求直线CM与D1N所成角的余弦值.
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(2)以D为坐标原点,以DA,DC,DD1分别为X,Y,Z轴正方向建立空间坐标系D-xyz,分别求出CM与D1N的方向向量,代入向量夹角公式,即可求出CM与D1N所成角的余弦值.
解答:
(1)证明:以D为坐标原点,以DA,DC,DD1分别为X,Y,Z轴正方向建立空间坐标系D-xyz,如图
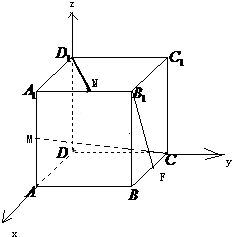
设正方体的棱长为2,则D1(0,0,2)、N(2,2,1)、B1(2,2,2)、F(1,2,0),
=(2,2,-1),
=(-1,0,-2)
所以
•
=-2+0+2=0,
所以D1N垂直B1F;
(2)解:以D为坐标原点,以DA,DC,DD1分别为X,Y,Z轴正方向建立空间坐标系,D-xyz,
∵正方体ABCD-A1B1C1D1的棱长为2,M,N分别为AA1、BB1的中点
则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
∴
=(2,-2,1),
=(2,2,-1)
∴cos<
,
>=
=
,
所以CM与D1N所成的角的余弦值为
.

设正方体的棱长为2,则D1(0,0,2)、N(2,2,1)、B1(2,2,2)、F(1,2,0),
| D1N |
| B1F |
所以
| D1N |
| B1F |
所以D1N垂直B1F;
(2)解:以D为坐标原点,以DA,DC,DD1分别为X,Y,Z轴正方向建立空间坐标系,D-xyz,
∵正方体ABCD-A1B1C1D1的棱长为2,M,N分别为AA1、BB1的中点
则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
∴
| CM |
| D1N |
∴cos<
| CM |
| D1N |
| ||||
|
|
| -1 |
| 9 |
所以CM与D1N所成的角的余弦值为
| 1 |
| 9 |
点评:本题考查了正方体为载体的线线垂直的判定和异面直线所成的角的求法;本题借助于空间向量的数量积解答的,注意题目的转化方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=log2(-x2+x+6)的单调减区间是( )
A、(-∞,
| ||
B、[
| ||
C、(-2,
| ||
D、(
|
 在如图所示的图形上画一条直线,使下面的图形划为两个三角形.
在如图所示的图形上画一条直线,使下面的图形划为两个三角形.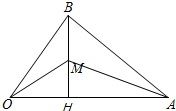
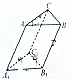 已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.
已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.