题目内容
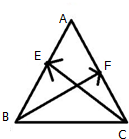 如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求
如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求| CE |
| BF |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由于E、F分别是AB、AC的中点,则
=
(
+
),
=
(
+
).运用向量的数量积的定义,化简即可得到.
| CE |
| 1 |
| 2 |
| CA |
| CB |
| BF |
| 1 |
| 2 |
| BA |
| BC |
解答:
解:由于E、F分别是AB、AC的中点,
则
=
(
+
),
=
(
+
).
则
•
=
(
+
)•(
+
)=
(
+
)•(
-2
)
=
2-
2-
•
=
×4-
×4-
×2×2×
=-
.
则
| CE |
| 1 |
| 2 |
| CA |
| CB |
| BF |
| 1 |
| 2 |
| BA |
| BC |
则
| CE |
| BF |
| 1 |
| 4 |
| CA |
| CB |
| BA |
| BC |
| 1 |
| 4 |
| CA |
| CB |
| CA |
| CB |
=
| 1 |
| 4 |
| CA |
| 1 |
| 2 |
| CB |
| 1 |
| 4 |
| CA |
| CB |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查向量的数量积的定义和性质,考查向量的加减运算,以及中点向量的表示形式,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列函数中是奇函数是( )
A、y=x3-x+
| ||||||
B、y=
| ||||||
| C、y=x4-x2 | ||||||
| D、y=x6+x2+2 |
函数y=|cosx|的最小正周期是( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
若用下列四个函数中的一个来描述这些数据的规律,则其中最接近的一个是( )
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y(台) | 10 | 20 | 39 | 81 | 160 |
| A、f(x)=10x |
| B、f(x)=5x2-5x+10 |
| C、f(x)=5•2x |
| D、f(x)=10log2x+10 |
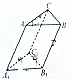 已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.
已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.