题目内容
已知直角坐标系xOy中,直线l的参数方程:
(t为参数),以直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,则以极点为圆心与直线l相切的圆的极坐标方程为 .
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:直线l的参数方程:
(t为参数),消去参数t可得x=y-
.利用点到直线的距离公式可得:原点到直线的距离r=
=1.即可得出圆的方程.
|
| 2 |
| ||
|
解答:
解:直线l的参数方程:
(t为参数),消去参数t可得x=y-
.
∴原点到直线的距离r=
=1.
∴以极点为圆心与直线l相切的圆的极坐标方程为 ρ=1.
故答案为:ρ=1.
|
| 2 |
∴原点到直线的距离r=
| ||
|
∴以极点为圆心与直线l相切的圆的极坐标方程为 ρ=1.
故答案为:ρ=1.
点评:本题考查了把直线的参数方程化为普通方程、直角坐标方程化为极坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
在△ABC中,已知∠BAC=150°,且
•
=-4
,设D是△ABC内部的一点,△DAB、△DBC、△DCA的面积依次为m、n、p,则当p=1时,
+
的最小值为( )
| AB |
| AC |
| 3 |
| 1 |
| m |
| 4 |
| n |
| A、3 | B、5 | C、7 | D、9 |
已知函数f(x)=
,如果f(x0)=2,那么实数x0的值为( )
|
| A、4 | B、0 | C、1或4 | D、1或-2 |
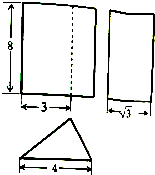 设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于
设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于 定义在区间[-
定义在区间[-