题目内容
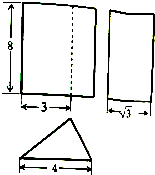 设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于
设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据已知中的三视图,可又判断该几何体是一个棱柱,由棱柱及球的几何特征可得球心距为棱柱高的一半,由正弦定理可求出底面外接圆半径,进而求出球半径,代入球的表面积公式,可得答案.
解答:
解:由已知中的三视图,可得该几何体是一个三棱柱,
底面的半径r满足2r=4,
则r=2,
棱柱的高为8,
则球心到底面的距离d=4,
则球的半径R=
=2
,
故此球的表面积S=4πR2=80π,
故答案为:80π.
底面的半径r满足2r=4,
则r=2,
棱柱的高为8,
则球心到底面的距离d=4,
则球的半径R=
| r2+d2 |
| 5 |
故此球的表面积S=4πR2=80π,
故答案为:80π.
点评:本题考查的知识点是由三视图求面积,棱柱的几何特征,圆内接多面体,其中根据已知求出球心距及棱柱底面外接圆半径,进而求出球半径是解答的关键.

练习册系列答案
相关题目
已知数列{an}的首项a1=1,an+1=3Sn(n∈N*),则下列结论正确的是( )
| A、数列是{an}等比数列 |
| B、数列a2,a3,…,an是等比数列 |
| C、数列是{an}等差数列 |
| D、数列a2,a3,…,an是等差数列 |
设非零向量
、
、
满足|
|=|
|=|
|,
+
=
,则
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、150° | B、120° |
| C、90° | D、60° |
某程序框图如下图所示,则该程序运行后输出S的值为( )

| A、10 | B、12 | C、15 | D、18 |
函数y=
的图象大致是( )
| x2 |
| ex-1 |
A、 |
B、 |
C、 |
D、 |
设a=
,b=
,c=
,则a,b,c的大小关系为( )
| e6 |
| 36 |
| e7 |
| 49 |
| e8 |
| 64 |
| A、a>b>c |
| B、b>a>c |
| C、c>b>a |
| D、c>a>b |