题目内容
在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,再将该小球放回箱子中摇匀后,乙从该箱子中摸出一个小球.
(Ⅰ)若甲、乙两人谁摸出的球上标的数字大谁就获胜(若数字相同为平局),求甲获胜的概率;
(Ⅱ)若规定:两人摸到的球上所标数字之和小于6则甲获胜,否则乙获胜,这样规定公平吗?
(Ⅰ)若甲、乙两人谁摸出的球上标的数字大谁就获胜(若数字相同为平局),求甲获胜的概率;
(Ⅱ)若规定:两人摸到的球上所标数字之和小于6则甲获胜,否则乙获胜,这样规定公平吗?
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由题意知本题是一个古典概型,列举出所有的基本事件,列举出满足条件的事件,根据古典概型的公式,得到结果.
(2)根据古典概型公式算出两人摸到的球上所标数字之和小于6则甲获胜,否则乙获胜,把所得结果进行比较,得到结论.
(2)根据古典概型公式算出两人摸到的球上所标数字之和小于6则甲获胜,否则乙获胜,把所得结果进行比较,得到结论.
解答:
解:用(x,y)(x表示甲摸到的数字,y表示乙摸到的数字)表示甲、乙各摸一球构成的基本事件,则基本事件有:(1,1),(1,2)、(1,3)、(1,4)、(1,5)、(2,1)、(2,2)、(2,3)、(2,4)、(2、5)、(3,1)、(3,2)、(3,3)、(3,4)、(3、5)、(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(5,1)、(5,2)、(5,3)、(5,4)、(5,5)共25个;
(1).则事件A包含的基本事件有:(2,1)、(3,1)(3,2)(4,1)(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4)、共有10个;
则 P(A)=
=
.)
(2).设:甲获胜的事件为B,乙获胜的事件为C.事件B所包含的基本事件有:事件B所包含的基本事件有:(1,1),(1,2)、(1,3),(1,4),(2,1),(2,2),(2.3),(3,1),(3,2),(4,1)共有10个;
则P(B)=
=
所以P(C)=1-P(B)=1-
=
.
因为P(B)≠P(C),所以这样规定不公平.
(1).则事件A包含的基本事件有:(2,1)、(3,1)(3,2)(4,1)(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4)、共有10个;
则 P(A)=
| 10 |
| 25 |
| 2 |
| 5 |
(2).设:甲获胜的事件为B,乙获胜的事件为C.事件B所包含的基本事件有:事件B所包含的基本事件有:(1,1),(1,2)、(1,3),(1,4),(2,1),(2,2),(2.3),(3,1),(3,2),(4,1)共有10个;
则P(B)=
| 10 |
| 25 |
| 2 |
| 5 |
所以P(C)=1-P(B)=1-
| 2 |
| 5 |
| 3 |
| 5 |
因为P(B)≠P(C),所以这样规定不公平.
点评:本题考查概率的意义和用列举法来列举出所有的事件数,本题解题的关键是不重不漏的列举出所有的事件数.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
设函数g(x)满足g(x+2)=g(2-x),f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有三个不同的实数解x1,x2,x3,则x1+x2+x3=( )
|
| A、0 | B、2 | C、4 | D、6 |
设非零向量
、
、
满足|
|=|
|=|
|,
+
=
,则
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、150° | B、120° |
| C、90° | D、60° |
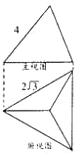 已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为
已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为