题目内容
已知正方体ABCD-A1B1C1D1的棱长为1，点P是右侧面CDD1C1上的一个动点，满足
•
=1，则点P的轨迹为 ．
| BA1 |
| BP |
考点：平面向量数量积的运算
专题：计算题,向量法
分析：以D为坐标原点，DA，CD，DD1为x，y，z轴建立直角坐标系，设P（0，y，z），由于A1（1，0，1），B（1，1，0），求出向量BP，BA1的坐标，运用向量的数量积的坐标公式，得到方程，即可判断轨迹．
解答：
解：以D为坐标原点，DA，CD，DD1为x，y，z轴建立直角坐标系，
设P（0，y，z），由于A1（1，0，1），B（1，1，0），
则
=（0，-1，1），
=（/-1，y-1，z），
•
=1-y+z=1，
则有y=z．
则点P的轨迹为直线y=z．
故答案为：直线
解：以D为坐标原点，DA，CD，DD1为x，y，z轴建立直角坐标系，设P（0，y，z），由于A1（1，0，1），B（1，1，0），
则
| BA1 |
| BP |
| BA1 |
| BP |
则有y=z．
则点P的轨迹为直线y=z．
故答案为：直线
点评：本题考查空间向量的数量积的坐标公式，考查点的轨迹及运算能力，属于基础题．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
甲、乙两个同学分别解一道一元二次方程，甲因把一次项系数看错了，而解得方程两根为-3和5，乙把常数项看错了，解得两根为2+
和2-
，则原方程是（ ）
| 6 |
| 6 |
| A、x2+4x-15=0 |
| B、x2-4x+15=0 |
| C、x2+4x+15=0 |
| D、x2-4x-15=0 |
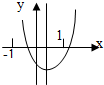已知二次函数f（x）=ax2+bx+c（a≠0）的图象如图所示，设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b，则（ ）| A、M＞0 | B、M≥0 |
| C、M＜0 | D、M=0 |
如图，在△ABC中，∠C=90°，点E是AC上一点，ED⊥AB，cosA=已知函数f（x）≠1，且对定义域内任意x总有关系[f（x+π）+1]•[f（x）+1]=2，那么下列结论中正确的是（ ）
| A、f（x）是周期为π的周期函数 | ||
| B、f（x）是周期为2π的周期函数 | ||
C、f（x）是周期为
| ||
| D、f（x）不是周期函数 |
