题目内容
若对一切的实数x,有3x2-2mx-1≥|x|-
成立,求实数m的取值范围.
| 7 |
| 4 |
考点:函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:对x讨论,当x=0时,不等式显然成立;当x>0时,原不等式即为3x2-2mx-1≥x-
,即2m+1≤3(x+
),恒成立,运用均值不等式求出右边的最小值;当x<0时,原不等式即为3x2-2mx-1≥-x-
,即2m-1≥3(x+
),恒成立,运用均值不等式求出右边的最大值.最后求交集即可.
| 7 |
| 4 |
| 1 |
| 4x |
| 7 |
| 4 |
| 1 |
| 4x |
解答:
解:当x=0时,不等式即为-1≥-
,成立;
当x>0时,原不等式即为3x2-2mx-1≥x-
,
即2m+1≤3(x+
),恒成立,由于x+
≥2
=1,
当且仅当x=
取最小值1,则2m+1≤3,解得,m≤1;
当x<0时,原不等式即为3x2-2mx-1≥-x-
,
即2m-1≥3(x+
),恒成立,由于x+
≤-2
=-1,
当且仅当x=-
,取最大值-1,则2m-1≥-3,解得m≥-1,
由于对一切的实数x,原不等式恒成立,
则实数m的取值范围是[-1,1].
| 7 |
| 4 |
当x>0时,原不等式即为3x2-2mx-1≥x-
| 7 |
| 4 |
即2m+1≤3(x+
| 1 |
| 4x |
| 1 |
| 4x |
x•
|
当且仅当x=
| 1 |
| 2 |
当x<0时,原不等式即为3x2-2mx-1≥-x-
| 7 |
| 4 |
即2m-1≥3(x+
| 1 |
| 4x |
| 1 |
| 4x |
x•
|
当且仅当x=-
| 1 |
| 2 |
由于对一切的实数x,原不等式恒成立,
则实数m的取值范围是[-1,1].
点评:本题考查不等式的恒成立问题,注意运用参数分离,转化为求函数的最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
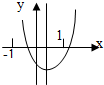 已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )
已知二次函数f(x)=ax2+bx+c(a≠0)的图象如图所示,设M=|a+b+c|-|a-b+c|+|2a+b|-|2a-b,则( )| A、M>0 | B、M≥0 |
| C、M<0 | D、M=0 |
 如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,面AB1M∥面BC1N,CA∩面BC1N=N.求证:N为AC的中点.
如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,面AB1M∥面BC1N,CA∩面BC1N=N.求证:N为AC的中点. 如图,在△ABC中,∠C=90°,点E是AC上一点,ED⊥AB,cosA=
如图,在△ABC中,∠C=90°,点E是AC上一点,ED⊥AB,cosA=