题目内容
4.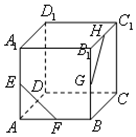 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
分析 先通过平移将两条异面直线平移到同一个起点B,得到的锐角∠A1BC1就是异面直线所成的角,在三角形A1BC1中求出此角即可.
解答  解:如图,连A1B、BC1、A1C1,则A1B=BC1=A1C1,
解:如图,连A1B、BC1、A1C1,则A1B=BC1=A1C1,
且EF∥A1B、GH∥BC1,
锐角∠A1BC1就是异面直线所成的角,
所以异面直线EF与GH所成的角等于60°,
故选:B.
点评 本题主要考查了异面直线及其所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$\sqrt{3}$,AB=2$\sqrt{2},AC=\sqrt{2},∠BAC={60°}$,则此球的体积等于( )
| A. | $\frac{{8\sqrt{2}π}}{3}$ | B. | $\frac{9π}{2}$ | C. | $\frac{{5\sqrt{10}π}}{3}$ | D. | $\frac{{4\sqrt{3}π}}{3}$ |
12.已知m∈R,“方程ex+m-1=0有解”是“函数y=logmx在区间(0,+∞)为减函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.“m>n>0”是方程mx2+ny2=1表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.如果实数x,y满足(x-2)2+y2=2,则$\frac{y}{x}$的范围是( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
14.不等式2x2-x>0的解集是( )
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
 函数f(x)在其定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象为( )
函数f(x)在其定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象为( )



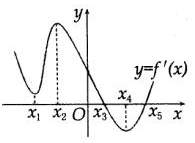 如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )
如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )