已知m∈R.“方程ex+m-1=0有解是“函数y=logmx在区间A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件题目和参考答案——青夏教育精英家教网—

题目内容

12．已知m∈R，“方程e^x+m-1=0有解”是“函数y=log_mx在区间（0，+∞）为减函数”的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

分析方程e^x+m-1=0有解，则m=1-e^x＜1．函数y=log_mx在区间（0，+∞）为减函数，则0＜m＜1．即可判断出结论．

解答解：方程e^x+m-1=0有解，则m=1-e^x＜1．
函数y=log_mx在区间（0，+∞）为减函数，则0＜m＜1．
“方程e^x+m-1=0有解”是“函数y=log_mx在区间（0，+∞）为减函数”的必要不充分条件．
故选：B．

点评本题考查了函数的单调性、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案

河南各地名校期末试卷精选系列答案

优等生练考卷单元期末冲刺100分系列答案

花山小状元课时练初中生100全优卷系列答案

一课一练文心出版社系列答案

海豚图书中考必备系列答案

A．

$y=tan（{2x+\frac{π}{6}}）$

B．

$y=cot（{x-\frac{π}{6}}）$

C．

$y=tan（{2x-\frac{π}{6}}）$

D．

y=tan2x

12．数列{a_n}中，a_2n=a_2n-1+（-1）ⁿ，a_2n+1=a_2n+n，a₁=1，则a₂₀=46．

9．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y+6≥0}\\{x≤3}\\{x+y+k≥0}\end{array}\right.$，且z=2x+4y的最小值为2，则常数k=（　　）

7．抛物线x²=4y的焦点为F，过点（0，-1）作直线交抛物线于不同两点A，B，以AF，BF为邻边作平行四边形FARB，求顶点R的轨迹方程．

17．已知f（x）=ax²+x-a，a∈R
（Ⅰ）若a=1，解不等式f（x）＞1
（Ⅱ）若a＜0，解不等式f（x）＞1．

4．

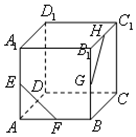如图，在正方体ABCD-A₁B₁C₁D₁中，E，F，G，H分别为AA₁，AB，BB₁，B₁C₁的中点，则异面直线EF与GH所成的角等于（　　）

1．设命题p：f（x）=x²+（2m-2）x+3在区间（-∞，0）上是减函数；命题q：“不等式x²-4x+1-m≤0无解”．如果命题p∨q为真，命题p∧q为假，求实数m的取值范围．

2．若$tanθ=-\frac{1}{3}，θ∈（\frac{π}{2}，π），则cos2θ$=（　　）

试题分类