题目内容
13.如果实数x,y满足(x-2)2+y2=2,则$\frac{y}{x}$的范围是( )| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
分析 设$\frac{y}{x}$=k,求$\frac{y}{x}$的范围就等价于求同时经过原点和圆上的点的直线中斜率的范围,由数形结合法,易得答案.
解答 解:设$\frac{y}{x}$=k,则y=kx表示经过原点的直线,k为直线的斜率.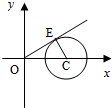
所以求$\frac{y}{x}$的范围就等价于求同时经过原点和圆上的点的直线中斜率的范围.
从图中可知,斜率取最大值时对应的直线斜率为正且与圆相切,
此时的斜率就是其倾斜角∠EOC的正切值.
易得|OC|=2,|CE|=$\sqrt{2}$,可由勾股定理求得|OE|=$\sqrt{2}$,
于是可得到k=1,即为$\frac{y}{x}$的最大值.
同理,$\frac{y}{x}$的最小值为-1,
故选B.
点评 本题考查直线与圆的位置关系,数形结合是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.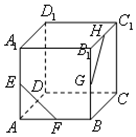 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
8.设m,n是两条不同的直线,α,β是两个不同的平面,下列说法正确的是( )
| A. | 若m∥α,α∩β=n,则 m∥n | B. | 若m∥α,m⊥n,则n⊥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若m?α,n?β,α⊥β,则m⊥n |
18.已知点P(t,t-1),t∈R,点E是圆x2+y2=$\frac{1}{4}$上的动点,点F是圆(x-3)2+(y+1)2=$\frac{9}{4}$上的动点,则|PF|-|PE|的最大值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
2.若$tanθ=-\frac{1}{3},θ∈(\frac{π}{2},π),则cos2θ$=( )
| A. | $-\frac{4}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
3.将一颗骰子连续抛掷2次,则向上的点数之和为8的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{5}{36}$ | C. | $\frac{3}{18}$ | D. | $\frac{1}{72}$ |
 在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.