题目内容
6.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
分析 (Ⅰ)由频率分布表能求出a,b,c的值.
(Ⅱ)依题意可知,微信群个数超过15个的概率为p=$\frac{2}{5}$. X的所有可能取值0,1,2,3.分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由已知得:0+30+30+a+5=100,解得a=35,
∴$b=\frac{5}{100}=0.05,c=\frac{35}{100}=0.35$.…(3分)
(Ⅱ)依题意可知,微信群个数超过15个的概率为p=$\frac{2}{5}$. …(4分)
X的所有可能取值0,1,2,3. …(5分)
则P(X=0)=${C}_{3}^{0}(\frac{2}{5})^{0}(1-\frac{2}{5})^{3}$═$\frac{27}{125}$,
P(X=1)=${C}_{3}^{1}(\frac{2}{5})(1-\frac{2}{5})^{2}$=$\frac{54}{125}$,
P(X=2)=${C}_{3}^{2}(\frac{2}{5})^{2}(1-\frac{2}{5})$=$\frac{36}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{2}{5})^{3}(1-\frac{2}{5})^{0}$=$\frac{8}{125}$. …(8分)
其分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
EX=$0×\frac{27}{125}+1×\frac{54}{125}+2×\frac{36}{125}+3×\frac{8}{125}$=$\frac{6}{5}$. …(12分)
点评 本题考查概率的求法,考查频率分布表、离散型随机变量的分布列、数学期望等基础知识,考查运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.△ABC的三个内角为A、B、C,若$\frac{{sinA+\sqrt{3}cosA}}{{cosA-\sqrt{3}sinA}}=tan\frac{7π}{12}$,则sin2B+2cosC的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
1.若直线x+2y+a=0过圆x2+y2+2x-4y+1=0的圆心,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
15.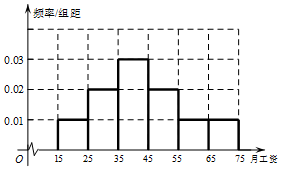 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:| 月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
| 女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
 在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.
在四棱锥P-ABCD中,已知DC∥AB,DC=2AB,E为棱PD的中点.