题目内容
18.已知函数f(x)=x3+3ax2.(Ⅰ) 若a=-1,求f(x)的极值点和极值;
(Ⅱ) 求f(x)在[0,2]上的最大值.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间和极值即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的最大值即可.
解答 解:(Ⅰ)a=-1时,f(x)=x3-3x2,
f′(x)=3x2-6x=3x(x-2),
令f′(x)>0,解得:x>2或x<0,
令f′(x)<0,解得:0<x<2,
故f(x)在(-∞,0)递增,在(0,2)递减,在(2,+∞)递增;
故x=0是极大值点,极大值是f(0)=0,
x=2是极小值点,极小值是f(2)=-4;
(Ⅱ)f′(x)=3x2+6ax=3x(x+2a),
a≥0时,f′(x)≥0,f(x)在[0,2]递增,
故f(x)max=f(2)=12a+8;
-1<a<0时,-2<2a<0,
令f′(x)>0,解得:x>-2a,
令f′(x)<0,解得:0<x<-2a,
故f(x)在[0,-2a)递减,在(-2a,2]递增,
故f(x)max=f(0)=0或f(2)=12a+8;
a≤-1时,2a≤-2,f(x)在[0,2]递减,
故f(x)max=f(0)=0.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.

练习册系列答案
相关题目
6.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
| 微信群数量 | 频数 | 频率 |
| 0至5个 | 0 | 0 |
| 6至10个 | 30 | 0.3 |
| 11至15个 | 30 | 0.3 |
| 16至20个 | a | c |
| 20个以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
13.已知函数f(x)在R上可导,其部分图象如图所示,设$\frac{f(2)-f(1)}{2-1}=a$,则下列不等式正确的是( )

| A. | a<f'(1)<f'(2) | B. | f'(1)<a<f'(2) | C. | f'(2)<f'(1)<a | D. | f'(1)<f'(2)<a |
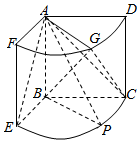 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点. 已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,
已知$\overrightarrow{a}$=2(cosωx,cosωx),$\overrightarrow{b}$=(cosωx,$\sqrt{3}$sinωx)(其中0<ω<1),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,