题目内容
8.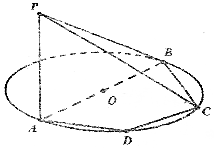 如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.
如图,PA⊥⊙O面,PA=2,AB为⊙O的直径,其长为4,四边形ABCD内接于圆O,且∠ADC=120°.(1)求点C到平面PAB的距离;
(2)当D在$\widehat{AC}$上什么位置时,BC∥平面POD;
(3)在(2)的条件下,求二面角D-PC-B的正切值.
分析 (1)作CE⊥AB,则CE⊥平面PAB,CE为点C到平面PAB的距离;
(2)当D在$\widehat{AC}$上中点位置时,BC∥平面POD.证明BC∥OD即可;
(3)作DM⊥AC于M,过M作MN⊥PC,由三垂线定理得∠MND为二面角D-PC-A的平面角.
解答  解:(1)作CE⊥AB,则CE⊥平面PAB,
解:(1)作CE⊥AB,则CE⊥平面PAB,
∴CE为点C到平面PAB的距离,
连接AC,则AC⊥BC,∠B=60°,
∵AB=4,∴BC=2,
∴CE=$\sqrt{3}$,即点C到平面PAB的距离为$\sqrt{3}$;
(2)当D在$\widehat{AC}$上中点位置时,BC∥平面POD.
∵D在$\widehat{AC}$上中点位置时,∠DAB=60°,
∴DC∥AB,DC=AD=$\frac{1}{2}$AB=OB,
∴OBCD是平行四边形,
∴BC∥OD,
∵BC?平面POD,OD?平面POD,
∴BC∥平面POD;
(3)作DM⊥AC于M,过M作MN⊥PC,由三垂线定理得∠MND为二面角D-PC-A的平面角.
在△MND中,求得tan∠MND=$\frac{\sqrt{3}}{2}$,
∵BC⊥AC,BC⊥PA,AC∩PA=A,∴BC⊥平面PAC,
∴二面角D-PC-B的正切值=tan(90°+∠MND)=-$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面垂直、线面平行的证明,考查空间角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.已知集合A={x|log2x<1},B={y|y=2x,x≥0},则A∩B=( )
| A. | ∅ | B. | {x|1<x<2} | C. | {x|1≤x<2} | D. | {x|1<x≤2} |
13.在△ABC中,若b2+c2-a2=bc,则角A的值为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
18.中石化集团通过与安哥拉国家石油公司合作,获得了安哥拉深海油田区块的开采权,集团在某些区块随机初步勘探了部分口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井.以节约勘探费用.勘探初期数据资料见如表:
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有的出油量不低于50L的井中任意勘察3口井,求恰有2口是优质井的概率.
| 井号I | 1 | 2 | 3 | 4 | 5 | 6 |
| 坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
| 钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
| 出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(2)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有的出油量不低于50L的井中任意勘察3口井,求恰有2口是优质井的概率.
 如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.
如图,正方形ABCD的边长为4,点E,F分别为边AB,BC上的动点,且DE=DF.


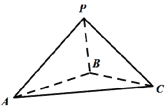 如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.
如图所示,四面体P-ABC中,$∠APB=∠BPC=∠CPA=\frac{π}{2}$,PA=4,PB=2,$PC=\sqrt{5}$,则四面体P-ABC的外接球的表面积为25π.